Unghiul dintre vectori, și exemple de formula

Determinarea formulei și unghiul dintre vectori

Unghiul dintre doi vectori și având o origine comună, - cel mai mic unghiul la care trebuie să se rotească în jurul vectorii punctului de aplicare în poziția în care va fi codirectional cu un alt vector (figura 1.).

Cosinusul unghiului dintre vectorii și produsul scalar al vectorilor este împărțit de produsul modulelor (lungime) a acestor vectori, adică

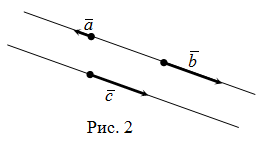
Dacă vectorii sunt coliniari, atunci unghiul dintre ele este egal cu (în figura 2, unghiul dintre vectorii u). Unghiul dintre vectori este egal orientate opus (dacă vectorii și au început să combine reprezentat în figura 2, atunci părțile ei sunt unghi drept).

Exemple de găsirea unghiurilor dintre vectori

Găsiți unghiul dintre vectorii și

La început vom calcula produsul scalar al vectorilor specificate, este egală cu suma produselor de origine factori ai vectorilor corespunzătoare:

Modulele vectorilor sunt date cu rădăcina pătrată a sumei pătratelor coordonate:

Apoi cosinusul unghiului dorit

Și apoi unghiul în sine

Găsiți cosinusul unghiului dintre vectorii și, dacă

Noi găsim coordonatele vectorilor și, în acest scop, coordonatele fiecărui capăt vector de coordonate corespunzătoare începe să-l scădere:

cosinusul unghiului dintre vectorii menționați se calculează cu formula cautata:

Astfel, obținem