Studiul funcției și construcția a graficului său

1) Funcția este definită pe toată axa reală, adică.

2) Punctele de intersecție ale graficului funcției cu axele de coordonate.

Intersecția axei. Functia are trei puncte de intersecție cu axele :.

3) non-periodică a funcției.

Funcția Odd, astfel încât graficul funcției este simetrică în raport cu originea.

4) Găsiți asimptota funcțiilor graficului. Funcția nu are puncte de pauză, astfel încât nu există nici o asimptotă verticală.

Găsim panta asimptota, în cazul în care

Panta asimptota, fie.

5) Găsim o funcție extremum și ascendent spațierea, descendent. Pentru a face acest lucru, vom calcula primul derivat

Punctele critice, echivalând primul derivat de zero:

Aceste puncte împart domeniului în patru intervale. Găsiți semnul derivatului în fiecare dintre intervalele și rezultatele sunt prezentate în tabelul de mai jos:

Punctul - punctul maxim, punctul de - punctul de minim.

6) Găsiți punctul de inflexiune, intervale de convexitate și concavitate. Pentru aceasta vom găsi derivata a doua

Punctele critice. Pentru a echivala acest al doilea derivat de la zero:

puncte găsite împărțiți domeniului în patru intervale. Am găsit semnul derivatei a doua la fiecare interval, iar rezultatele prezentate în tabel:

Valoarea funcției în punctele de inflexiune

7) Pe baza datelor obținute, am complot funcție.

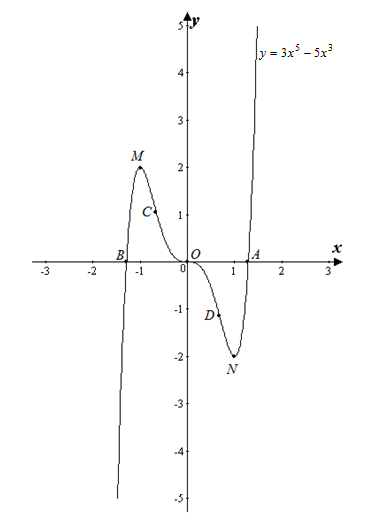
Pentru a investiga funcția și construi graficul acesteia.

1) Găsiți domeniul funcției. O funcție este o fracțiune rațională, prin urmare, pentru a exclude valoarea este resetat la zero, la numitor.

Astfel, domeniul funcției:

2) punctele de intersecție cu graficul axelor de coordonate:

Astfel, funcția trece prin origine - punct.

3) nu este periodică. Noi examinăm funcția de paritate:

Nici unul dintre ecuațiile, sau nu, astfel încât funcția nu este nici măcar, nici ciudat. Graficul functiei va avea nici o simetrie.

La punctul de rupere funcției. Definim comportamentul unui punct în apropierea acestui punct

Astfel, - ecuația asymptotes verticale.

Găsim panta asimptota, în cazul în care

Obținem ecuația asimptote înclinate.

5) Găsim o funcție extremum și Spațiere de creștere și descreștere. Pentru a face acest lucru, vom calcula derivata, folosind regula de diferențiere parțială:

Punctele critice: if

Nu există nici o limitare, dar acest punct nu aparține domeniului de definiție. Găsiți semnul derivatului în fiecare dintre intervalele și rezultatele sunt prezentate în tabelul

Acesta este punctul - punctul de maxim.

6) Găsiți punctul de inflexiune, intervale de convexitate și concavitate. Pentru a face acest lucru, găsim al doilea derivat

Punctele critice: atunci când nu există pentru, dar acest punct nu aparține domeniului de definiție. Am găsit semnul derivatei a doua la fiecare interval, iar rezultatele prezentate în tabel: