Principiul relativității a lui Einstein și transformările Lorentz - studopediya

Una dintre cele mai importante constante fizice este viteza luminii în vid, adică viteza de propagare a undelor electromagnetice în spațiu liber de substanță. Această viteză nu depinde de frecvența undelor electromagnetice, și este acum acceptată Valorile egale cu C = 299792458 m / s.

In marea majoritate a cazurilor, această valoare cu o precizie suficientă poate fi luată ca c = 3 • 108 m / s - în care eroarea mai mică de 0,001.

Și că „trei sute de mii de kilometri pe secundă“ pentru viteza luminii este amintit de cei mai mulți dintre noi pentru viață. Să ne amintim că 300 000 km - este ordinul de mărime, distanța de la Pământ la Lună (sau mai precis, 380 000 km).

Astfel, semnalul radio ajunge de la pământ prin luna în timp ce puțin mai mult de o secundă.

Presupunerea că lumina călătorește nu este infinit, dar la o viteză finită, a vorbit timp de multe secole înainte de oameni au fost capabili să-l dovedească experimental. Acest lucru a fost realizat pentru prima dată în secolul al XVII-lea, atunci când observațiile astronomice de „nereguli“ ciudate în mișcare Io satelit al lui Jupiter poate fi explicată numai pe ipoteza unei viteze finit de propagare a luminii (de altfel, această primă încercare de a determina viteza luminii a dat rezultate mai mici cu

Este montat un fapt surprinzător - valoarea vitezei luminii nu depinde de faptul dacă, în raport cu un sistem de referință, acesta este determinat!

Acest fapt experimental contrazice legea adăugarea de viteze de Galileo, pe care le-am discutat în capitolul anterior și care pare evidentă și confirmate de observațiile noastre de zi cu zi. Dar lumina nu se supune acestei reguli naturale, aparent viteza plus - în ceea ce privește toți observatorii, indiferent de modul în care acestea au fost în mișcare, lumina se propagă cu aceeași viteză c = 299,793 km / s. Iar faptul că propagarea luminii - mișcarea câmpului electromagnetic, nu particule,

constând din atomi, nu joacă un rol aici. În derivarea legii plus viteza (9.2) nu a contat natura obiectului în mișcare.

Și, deși este imposibil de a găsi ceva de genul că, în cunoștințele și experiența anterioară acumulată, cu toate acestea, trebuie să recunoaștem acest fapt de experiență, amintindu-ne că este experiența este un criteriu decisiv al adevărului. Să ne amintim că ne confruntăm cu o situație similară la începutul cursului, atunci când se discută proprietățile spațiului. Apoi am observat că să ne imaginăm curbura spațiu tridimensional, noi - ființele tridimensionale -nevozmozhno. Dar ne-am dat seama că faptul că „prezența sau absența“ curburii poate fi setat în mod empiric: prin măsurarea, de exemplu, suma unghiurilor unui triunghi.

Ce modificări trebuie să fie făcute în înțelegerea noastră a proprietăților spațiului și timpului? Și în lumina acestor fapte se referă la transformarea lui Galileo? Este posibil să le schimbe, astfel încât acestea încă nu intră în conflict cu bun simț atunci când sunt utilizate pentru mișcările obișnuite ale corpurilor din jurul nostru și, în același timp, nu contrazice faptul constan viteza luminii în toate cadrele de referință?

Soluția fundamentală a acestor probleme aparține Albertu Eynshteynu, care a creat la începutul secolului XX,. Teoria specială a relativității (SRT) asociate natura neobișnuită a propagării luminii cu proprietățile fundamentale ale spațiului și timpului, se manifesta la o viteză comparabilă cu viteza luminii. În literatura de fizică modernă este adesea denumit simplu mecanicii relativiste.

Ulterior a construit Teoria generală a relativității a lui Einstein (RTG), în cazul în care proprietățile relație și interacțiunile gravitaționale spațiu-timp.

Baza stației de serviciu este format din două postulate. care sunt numite principiul relativității a lui Einstein și principiul constanța vitezei luminii.

principiul relativității a lui Einstein este o generalizare a principiului relativității galilean discutat în capitolul anterior, toate fără excepție (nu doar mecanic) fenomene naturale. Conform acestui principiu, toate legile naturii sunt aceleași în toate sistemele de referință inerțiale. Principiul relativitatii pot fi rezumate după cum urmează: toate ecuațiile care exprimă legile naturii sunt invariante în raport cu transformările de coordonate și de timp de la un sistem de referință inerțial la altul. (Să ne amintim că invarianta

Ecuațiile numit imutabilitatea speciilor prin înlocuirea în ele coordonatele și coordonatele temporale ale unui sistem de referință, iar cealaltă dată). Este clar că, în conformitate cu principiul relativității, Einstein nu există niciun experiment la toate nu poate fi instalat pentru a fi în mișcare sistemul „nostru“ de referință la o viteză constantă sau este staționar, sau mai precis, nu există nici o diferență între aceste stări. Galileo a postulat imposibilitatea, în principiu, numai pentru testele mecanice.

Principiul constanței (mai precis, invarianță) viteza de stări de lumină care viteza luminii în vid este aceeași pentru toate sistemele de referință inerțiale. După cum vom vedea în scurt timp, rezultă că - maximul tuturor posibile vitezele fizice.

Ambele postulate sunt o reflectare a faptelor experimentale: viteza luminii este independentă de mișcarea sursei sau a receptorului; De asemenea, nu depinde de mișcarea cadrului de referință în care experimentele au fost efectuate pe măsurarea lui. Principiul relativității se reflectă în recunoașterea faptului că nu numai (de distribuție a luminii), fenomenele mecanice, dar electromagnetice, ascultați în toate sistemele de referință inerțiale

de aceleași legi.

Din dispozițiile menționate mai sus implică o serie de concluzii importante în ceea ce privește proprietățile de spațiu și timp. În primul rând, ei urmează noile reguli ale tranziției de la un sistem de referință inerțial la altul, în care „evidente“ transformări galileeni sunt doar câteva cazuri particulare, puse în aplicare doar atunci când se deplasează la viteze mult mai mici decât c. Pentru a determina aceste noi reguli vor lua în considerare lumină ce se propagă de la o sursă punct situat la începutul sistemului fix de referință K (fig. 10.1 a).

Propagarea luminii poate fi reprezentat ca lumina fata de propagare având forma unei suprafețe sferice, în cadrul de referință, în raport cu care sursa de lumină este staționară. Dar, conform principiului relativității, lumină din față Einstein trebuie să fie sferică și, de asemenea, atunci când se observă în cadrul de referință, care este în uniformă mișcare rectilinie în raport cu sursa.

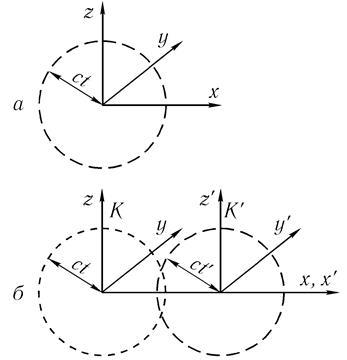
Fig. 10.1 răsaduri de lumină de la o sursă punct situat la începutul cadrului de referință staționar la partea din față a luminii să fie sferică și, de asemenea, atunci când se observă în cadrul de referință, care este în uniformă mișcare rectilinie în raport cu sursa.

Din această condiție ne acum definim ceea ce ar trebui să fie regulile de transformare a coordonatelor și de timp în tranziția de la un sistem inerțial la altul.

Dacă sursa de lumină este situat la începutul cadrului de referință K, lumina emisă la momentul t = 0, ecuația sferică luminoasă frontală are forma

x 2 + y 2 + z 2 = (ct) 2 (10,1)

Această ecuație descrie o suprafață sferică a cărei rază este R = ct

Timpul crește cu viteza.

Coordonatele și timpul măsurat de un observator în cadru K în mișcare „este notat cu PRIMES litere x“, y „z“, t“. Să presupunem că start calendarul t „coincide cu rama începutul t și că momentul zero coincizând sistem de coordonate top K1 coincide cu poziția sursei de lumină în sistemul K. Pentru a fi specific, sistemul K“ se deplasează în direcția + x, la o viteză constantă V în raport cu K (Fig. 10.1 b).

Așa cum am spus, în conformitate cu al doilea postulat al lui Einstein, pentru un observator în sistemul de lumină din față „amorsat“ ar trebui să fie, de asemenea, sferice, adică ecuația de lumină în fața sistemului de mișcare ar trebui să fie de forma

x '2 + y' 2 ​​+ z '2 = c 2 t' 2 (10.2)

în care viteza de cantitatea de lumină aici este aceeași cu cea în cadru K. De aceea, transformarea coordonatelor și timpul cadrului nostru audio la altul este necesar să posede o astfel de proprietate care, de exemplu, după înlocuirea acestor transformări (10.2) " „valori“ amorsate nu amorsată „trebuie să obținem din nou ecuația frontului sferic (10.1).

Este ușor de verificat că transformarea galilean (9.3) nu satisface această cerință. Să ne amintim că aceste transformări se referă coordonatele și timpul în două cadre diferite de referință următoarele relații:

x '= x - Vt, y' = y, z '= z, t' = t. (10.3)

Dacă înlocuim (10.3) în (10.2), obținem

x 2 - 2xVt + V 2 t 2 + y 2 + z 2 = c 2 t 2 (10,4)

care, desigur, nu este în concordanță cu ecuația (10.1). Ceea ce, atunci, trebuie să fie un nou convertit? În primul rând, din moment ce toate sistemele sunt egale, trecerea unui sistem de la orice alt ar trebui să fie descrise prin aceleași formule (cu valoarea V sale), o cerere de două ori a transformărilor prin înlocuirea a doua etapă la + V

-V ar trebui să ne întoarcem la sistemul original. Această proprietate poate avea doar liniară în raport cu x și t transformare. Este inutil de a testa pentru acest tip de relație

x „= x l / 2 t 1/2. x „= sin x

sau altele asemenea.

În al doilea rând, când V / s -> 0, transformarea trebuie să se deplaseze în transformarea Galileo, care este valabil pentru viteze joase nu poate fi pusă la îndoială.

Din ecuația (10.4), este clar că nu putem lăsa fără a schimba transformare t „= t, dacă doriți să distrugă această ecuație termeni nedoriți -2xVt + V 2 t 2. deoarece pentru a le distruge aveți nevoie pentru a fi sigur pentru a adăuga ceva de t .

Încercați mai întâi de transformare a formei:

x '= x-VT, y' = y, z '= z, t' = t + bx, (10.5)

unde b - o constantă a cărei valoare trebuie determinată. Apoi, ecuația (10.2) ia forma

x 2 - 2Vxt + V 2 t 2 + y 2 + z 2 = c 2 t 2 + 2c 2 bxt + c 2 b 2 x 2 (10.6)

Rețineți că termenii de pe partea stângă și dreaptă ale ecuației care conțin produsul xt, se anulează reciproc, dacă luați

b = -V / c 2. sau t „= t-Vx / c 2. (10,7)

La această valoare b, ecuația (10.6) poate fi rescrisă după cum urmează:

2 x (1 - V 2/2) + y 2 + z 2 = c 2 t 2 (l - V 2/2). (10,8)

Acest lucru este mai aproape de ecuația (10.1), dar rămâne încă un factor nedorit 1 - (V 2/2), care este multiplicată cu x 2 și t 2.

Putem exclude acest factor, dacă vom scrie transformarea finală a coordonatelor și a timpului, după cum urmează:

Aceasta este faimoasa transformare Lorentz, numit după fizicianul olandez Hendrik Lorentz teoretician, care în 1904 a condus formula (10,9) și astfel se pregătească trecerea la teoria relativității.

Este ușor de verificat că înlocuirea (10,9) în ecuația (10.2) transformarea Lorentz, așa cum ar trebui să fie, această ecuație este transformată într-o ecuație a suprafeței sferice (10.1) în sistemul de coordonate fix. De asemenea, este ușor de văzut că, atunci când

V / a -> 0 Lorentz continuă transformare în transformare Galileo (9.2).