Vectori și operații cu vectori

Vectorii ocupă un loc special printre obiectele considerate în matematici superioare, deoarece fiecare vector are nu numai o valoare numerică - lungimea, ci și fizic și geometric - orientarea. Vectorul reprezentat de segmentul de linie dirijat se extinde din punctul A la punctul B. notat cu.

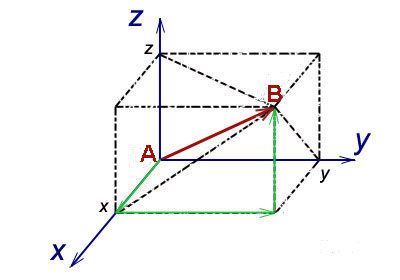
Vector - un tip de reprezentare a punctului la care este necesar accesul la un moment dat inițial. De exemplu, un vector tridimensional, de obicei scrise sub forma (x, y, z). Vorbind pur și simplu, aceste numere înseamnă, cât de departe vrei să mergi în trei direcții diferite, pentru a ajunge la punctul.

Fiind dat un vector. X = 3, în care (brațul drept îndreptat spre dreapta), y = 1 (stânga orientată înainte), z = 5 (punct stă sub scări care duc în sus). Din aceste date, veți găsi un punct de trecere de 3 metri în direcția indicată de mâna dreaptă, apoi 1 metru în direcția indicată de mâna stângă, și apoi sunt în așteptare pentru o scara si urca la 5 metri, în cele din urmă va ajunge la punctul dorit.

Toți ceilalți termeni - o explicație mai exactă prezentată mai sus, necesare pentru diverse operații pe vectori, adică, soluția problemelor practice. Mers pe jos în această definiție mai riguroasă, referindu-se la sarcinile tipice ale vectorilor.

Exemple fizice de cantități vectoriale pot servi ca o deplasare a unui punct material, se deplasează în spațiu, viteza și accelerarea acestui punct, precum și acționând asupra rezistenței acesteia.

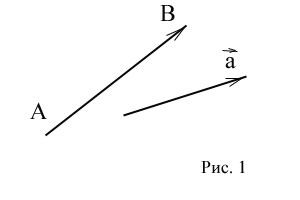
Vectorul geometric este reprezentat în bidimensional și spațiul tridimensional ca un segment de linie direcționată. și anume segment, care distinge începutul și sfârșitul.

Dacă A - începutul vectorului, și B - capătul său, vectorul notat cu unul sau o literă mică. Cifra indică sfârșitul săgeții vectorului (Fig. 1)

Lungimea (sau modul) este lungimea vectorului geometric generarea lungimii

Doi vectori se spune că sunt egale. în cazul în care acestea pot fi combinate (în direcții de coincidență) prin transfer paralel, și anume dacă acestea sunt paralele, ele sunt îndreptate spre una și aceeași direcție și au aceeași lungime.

În fizică, de multe ori considerate vectori consfințit. punct de aplicare predeterminat, lungimea și direcția. În cazul în care punctul de aplicare al vectorului nu contează, acesta poate fi transferat, menținând în același timp lungimea și direcția în orice punct din spațiu. În acest caz, vectorul este numit liber. Suntem de acord să ia în considerare vectori numai liberi.

Multiplicarea unui vector de un număr de

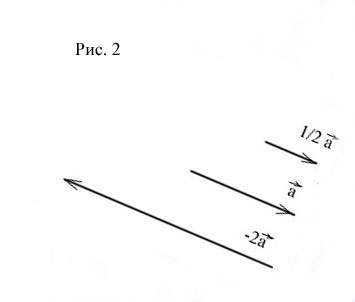
Vektorana numărul produsului este un vector obținut din vectorul de întindere (dacă) sau o contracție (în timp), în timp, cu direcția vectorului salvat dacă și invers, dacă. (Fig. 2)

Din definiția rezultă că vectorii u întotdeauna situate pe același sau pe linii paralele. Astfel de vectori sunt numite coliniare. (Se poate spune, de asemenea, că acești vectori sunt paralele, dar algebra vector pentru a spune „coliniare“.) Converse este de asemenea adevărat: dacă vectorii și sunt coliniari, atunci ele sunt legate de

Prin urmare, ecuația (1) exprimă condiția coliniaritate a doi vectori.

Adunare și scădere vectorilor

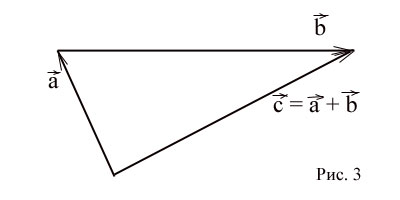
Când vectorii adăugând trebuie să știe că suma vectorilor este un vector al cărui început coincide cu începutul vectorului, iar la sfârșitul anului - la sfârșitul vectorului, cu condiția ca originea vectorului este aplicat la capătul vectorului. (Fig. 3)

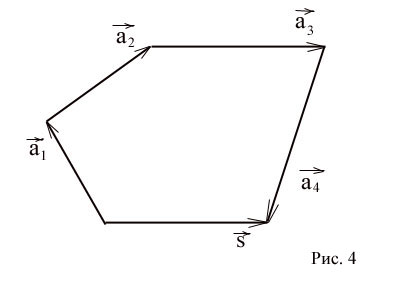
Această definiție poate fi distribuit la orice număr finit de vectori. In spatiul n sunt vectori liberi. La adăugarea mai multor vectori pentru a lua suma lor NO vector al cărui început coincide cu începutul primului vector, iar la sfârșitul - sfârșitul ultimului vector. Aceasta este, în cazul în care sfârșitul vectorului pentru a face vectorul începutul și sfârșitul vectorului - începutul vectorului, etc. și, în final, până la sfârșitul vectorului - începutul vectorului, suma acestor vectori este de închidere vector, al cărui început coincide cu începutul primului vector și sfârșitul - sfârșitul ultimului vector. (Fig. 4)

Termenii se numesc componente ale vectorului, și a formulat o regulă - regula poligonului. Acest poligon nu poate fi plat.

Multiplicată cu numărul de vectori obținut -1 vectorul opus. Vectorii au aceeași lungime și în direcții opuse. suma lor dă vectorul zero. a cărui lungime este egală cu zero. direcție vector zero nu este determinat.

In algebra vector nu trebuie luate în considerare separat scădere: scade din vector înseamnă un vector adăugat la vectorul opus vectorului, adică,

Exemplul 1: Simplificați expresia:

adică, pot fi adăugate vectori și multiplicat cu numărul cât și polinoamele (în special, problema este, de asemenea, pentru a simplifica expresiile). De obicei, necesitatea de a simplifica expresii liniare astfel de vectori se produce înainte de a calcula produse de vectori.

Exemplul 2. Vectori și servesc diagonalelor ABCD paralelogram (Fig. 4a). Exprimat în ceea ce privește vectorii, și care sunt părți la acest paralelogram.

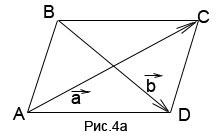
Decizie. Punctul de intersecție al diagonalelor unui paralelogram divide fiecare jumătate diagonală. Lungimile vectorilor dorite sunt fie ambii jumătate vectori sumă care formează un triunghi cu efectul dorit sau ca jumătate din diferența (în funcție de direcția de servire diagonală), sau, în acest din urmă caz, jumătate din suma, luat cu semnul minus. Astfel, vectorii necesari sunt:

Cum de a găsi lungimea suma vectorilor?

Această problemă are un loc special în operațiunile cu vectori, deoarece implică utilizarea proprietăților trigonometrice. Să presupunem că ați dat peste problema ca următoarele:

Având în vedere lungimea vectorilor și lungimea sumei acestor vectori. Găsiți lungimea diferenței dintre acești vectori.

Adresa acest lucru și alte probleme similare, și o explicație a modului în care să le rezolve - în lecția „Adăugarea de Vectorii: suma vectorială a lungimii și teorema cosinus“.

Și a verifica afară soluția de astfel de probleme pot fi afișate pe calculator on-line „din partea necunoscută a unui triunghi (adăugarea de vectori și teorema cosinus).“

În cazul în care produsele de vectori?

Produsul unui vector pentru vector este operațiuni neliniare și considerate separat. Și noi am învățat „produs scalar al vectorilor“ și „vector și produs în amestec de vectori“.

Proiecția vectorului pe axa este egală cu produsul dintre lungimea vectorului proiectat pe cosinusul unghiului dintre vectorul și axa:

După cum se știe, o proiecție a punctului A pe linia dreaptă (plan) este piciorul perpendicularei din acest punct la linia (planul).

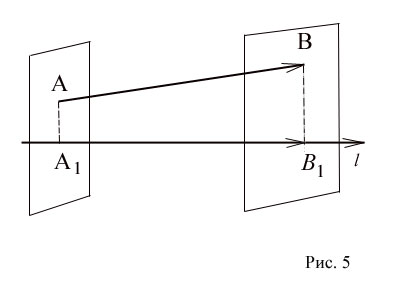
Să - vector arbitrar (Figura 5.) Și și - proeminențele începutul său (punctul A) și capătul (punctul B), pe l axa. (Pentru construcția punctului de proiecție A) pe linia prin punctul A plan perpendicular conduce linie. Intersecția liniei și planul va determina proiecția dorită.

L component axa vektorana se numește un vector situată pe axa, a cărei început coincide cu proiecția începutul și sfârșitul - sfârșitul proiecției vectorului.

Proiecția vectorului l pe axa este numărul

Lungimea vectorului este egală cu acea axă, luat cu semnul plus dacă sostavlyayushey direcție coincide cu direcția axei l. și cu un semn negativ, în cazul în care acestea sunt în direcții opuse.

Principalele proprietăți ale proeminențelor vectoriale pe axă:

1. Proiecțiile de vectori egale cu una și aceeași punte sunt egale.

2. Atunci când multiplicată cu numărul de proiecție vector este înmulțit cu același număr.

3. Proiecția sumei vectorului oricărei axe este egală cu suma proiecțiilor în aceleași condiții pe axa de vectori.

4. Proiecția vectorului pe axa este egală cu produsul dintre lungimea vectorului proiectat pe cosinusul unghiului dintre vectorul și axa:

Exemplul 3. Se calculează suma vectorială a proiecției pe axa l. dacă și colțuri -

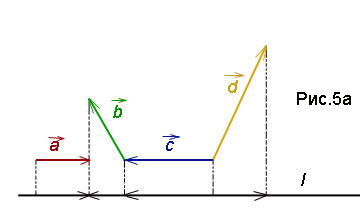
Decizie. proiect L vectorii așa cum sunt definite mai sus, în axa de ajutor teoretic. Din fig.5a evident că proiecția sumei vectorului este egală cu suma dintre proiecțiile vectorilor. Calculăm aceste proiecții:

Noi găsim proiecția necesară a sumei vectorului de:

Familiaritate cu cartezian rectangular sistem de coordonate în spațiul deținut în clasa corespunzătoare. este de dorit să-l deschidă într-o fereastră nouă.

Sistemul ordonat de axe de coordonate 0xyz axa Ox se numește axa orizontală. axa 0Y - axa y. iar axa 0Z - axa z.

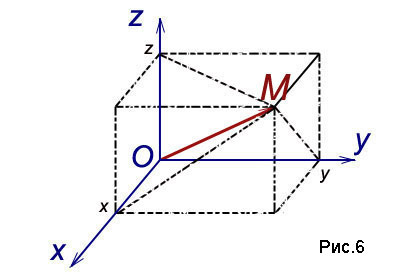
Cu un vector spațial M asociat punct arbitrar

numit vectorul raza punctului M și proiectează-l pe fiecare dintre axele de coordonate. Notăm valori proiecții corespunzătoare:

Numerele x, y, z coordonatele punctului sunt numite MA abscisă respectiv. ordonata si applicate. și este scris într-un numere de puncte ordonate: M (x, y, z) (Fig.6).

versorul a cărei direcție coincide cu direcția axei, se numește un vector unitate (sau vector unitate) axă. Vom nota cu

Prin urmare, vectorii unitare ale axelor de coordonate Ox. Oy. oz

Teorema. Orice vector poate fi descompus prin unități vectorii axelor de coordonate:

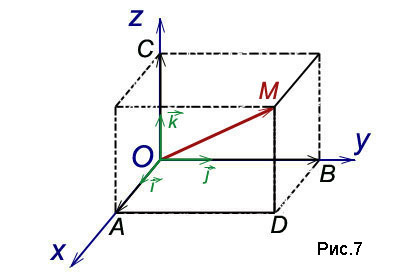
Ecuația (2) se numește vectori de descompunere a lungul axelor de coordonate. Coeficienții acestei extinderi sunt proiecții ale vectorului pe axele de coordonate. Astfel, coeficienții de dilatare (2) al vectorului pe axele de coordonate sunt coordonatele vectorului.

După selectarea unui sistem de coordonate anumit vector spațiu și originea triplu determină în mod unic reciproc, cu toate acestea, vectorul poate fi scrisă sub forma

Reprezentarea Vector in forma (2) și (3) sunt identice.

Așa cum am observat, vectorii se numesc coliniare în cazul în care acestea sunt legate de

Să presupunem că vectorii. Acești vectori sunt coliniari, dacă coordonatele vectorilor sunt legate de

adică, coordonatele vectorilor proporționale.

Exemplul 4 Date fiind vectorii. dacă acești vectori sunt coliniari?

Decizie. Să ne determine raportul dintre vectorii de coordonate de date:

Coordonatele vectorilor proporționale, prin urmare, vectorii sunt coliniari, sau ceea ce este același paralel.

n - vectori dimensionale și a operațiunilor de pe ele

În studiul de multe probleme, cum ar fi economice, este convenabil de a generaliza tehnicile discutate pentru cartografierea între numere și puncte de spațiu bidimensional și tridimensional și ia în considerare secvența de numere reale n ca „punct“ a unor abstracte „spațiu n-dimensional“, iar numerele în sine - ca " coordonatele „acestor puncte. Pentru componentele vectoriale n-dimensionale pot lua de date, cum ar fi productivitatea diferitelor culturi, volumul vânzărilor de mărfuri, factorii tehnici, gama de produse în depozite, etc.

n-dimensional vector este un set ordonat de numere reale n înregistrate sub formă de

unde - i - a vectorului x - elementul (th component sau i) th.

Există, de asemenea, un alt vector de intrare - sub forma unei coloane coordonate:

Dimensiunea vectorului este determinată de numărul de origine și este o caracteristică distinctivă. De exemplu, (2, 5) - vector dimensional (2, -3, 0) - tridimensional (1, 3, -2, -4, 7) - o perioadă de cinci-dimensional,

n - vectorul dimensional.

Vectorul zero este vectorul ale cărui coordonate sunt egale cu zero:

Prezentați operarea vectorilor n-dimensionale.

numărul real este un vector

și anume vector prin înmulțirea cu numărul fiecărei coordonate este înmulțită cu numărul respectiv.

puteți obține vectorul opus

și anume prin adăugarea vectorilor de aceeași dimensiune a coordonatelor corespunzătoare termwise adăugate.

În cazul în care condițiile de vânzare de rețea întreprinderi comerciale de vânzare de bunuri definite ca niveluri pozitive de bunuri și costul vânzărilor - negativ, obținem costurile vectoriale-vânzări

vânzări (cost) k - m-am produs acum. și k = 1, 2, 3, ..., m.

Vectorul costului total al vânzărilor se determină prin adăugarea vectorii de vânzări y-cost ale tuturor companiilor m rețea:

Suma vectorilor opuse conferă vectorului de zero:

Când scăzând doi vectori de aceeași dimensiune a coordonatelor corespunzătoare sunt scăzute pe termen de termen:

Manipulau vectori -dimensionale n îndeplinesc următoarele proprietăți.