Studiul complet al funcției și plotarea - studopediya

Un studiu complet al funcțiilor și programele lor de construcție convenabile pentru a efectua după cum urmează:

1) pentru a găsi o zonă de definiție de funcție;

2) a determina dacă funcția nu este par sau impar, periodic;

3) pentru a investiga continuitatea, pentru a găsi un punct de pauză și să clarifice natura discontinuităților;

4) pentru a găsi asimptota graficului;

5) explora monotonia funcției și de a găsi extremele ei;

6) Găsiți punctul de inflexiune, setați intervalele de convexitate și concavitate a graficului funcției;

7) reprezintă graficul punctelor suplimentare, de exemplu, punctul de intersecție cu axele de coordonate.

Rezultatul fiecărui element trebuie să se reflecte imediat pe programul și să fie în concordanță cu rezultatele cercetărilor cu privire la alineatele precedente.

Pentru a efectua un studiu complet al funcției și trage grafic.

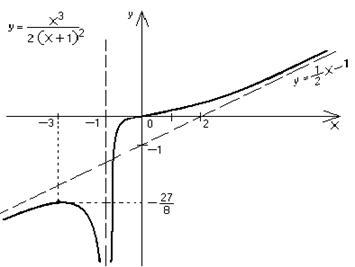
1. Funcția definită în intervalul xÎ (- ¥; 1) È (-1 + ¥).

2. Funcția nu poate fi chiar sau impar, deoarece domeniul său de definiție nu este simetrică în raport cu 0. Prin urmare, funcția de formă generală, adică, Paritatea nu posedă proprietăți. De asemenea, funcția nu este periodică.

Funcția se numește chiar. în cazul în care sunt îndeplinite două condiții:

a) domeniul său de definiție este simetrică în raport cu zero,

b) pentru toate valorile lui x în domeniul egalității.

Grafic chiar și funcția are o simetrie axială, în jurul unei axe OY.

Funcția se numește ciudat. dacă

a) domeniul său a funcției este simetrică în raport cu zero,

b) atunci când „x în domeniul definiției.

Funcția ciudat Graph are o simetrie relativă centrală a originii.

Funcția se numește periodică. în cazul în care există un număr T> 0 este astfel încât egalitatea „x în domeniul definiției.

Numărul T este perioada funcției. iar graficul acesteia este suficientă pentru a construi în orice interval de lungime T. și apoi extins periodic pentru întregul domeniu.

3. Funcția este continuă pentru toți xÎ (- ¥; -1) È (-1 + ¥).

Această funcție este o unitate care este format prin divizarea a două funcții continue și elementare de bază. Prin urmare, proprietățile funcțiilor continue, această funcție este continuă la toate punctele la care este definit.

X = -1 este punctul de fractură, deoarece în ea, această funcție nu este definită. Pentru a determina natura (tip) a diferenței, se calculează. În consecință, pentru x = -1 funcție are o discontinuitate infinită (II gap gen).

4. asimptotă funcțiilor graficului.

asimptotă verticală este linia x = -1 (aceasta rezultă din ruperea funcției de cercetare).

asimptotă înclinate în căutarea ecuație. unde

Astfel, - această ecuație asymptotes înclinată (la H® ± ¥).

5. Monotonia și extreme definesc funcția cu ajutorul primului său derivat:

Punctul critic este determinat de următoarele condiții:

condiții suficiente de monotonie și: extremele

6. Intervale de convexitate și concavitate a graficului unei funcții, punctul său de inflexiune este folosind derivata a doua:

Suspicios la punctul de inflexiune este determinată de următoarele condiții:

Condiții suficiente pentru punctele de convexitate, concavitate și flexiune:

Punctul O (0, 0) este punctul de inflexiune al graficului.

Rezultatele cercetării funcționează adesea cu ajutorul primului și al doilea derivat întocmește un tabel general, care prezintă principalele caracteristici ale graficului funcției:

Toate rezultatele activității de cercetare reflectă programul său.

OOF: xÎ (- ¥; -) È (-;) È (+ ¥).

Este o funcție ciudat, ca domeniu este simetrică în raport cu zero și „x Î OOF egalitatea:

Prin urmare, graficul funcției are o simetrie relativă centrală a originii.

Funcția este continuă pentru toți xÎ (- ¥; -) È (-;) È (+ ¥), ca Funcția elementară este continuă pe OOF acestuia. X = - = și x sunt puncte de discontinuitate infinite, deoarece,

asimptotă verticală a graficului sunt linii x = - și x =.

asimptotă :. Înclinat unde

- această ecuație asimptota oblică.

Intervale de creștere și descreștere a funcției, extremele sale.

Cerințe preliminare Extrema:

condiții suficiente de monotonie și: extremele

Intervale de convexitate, concavitatea graficul funcției și punctul de inflexiune:

Punctul x = 0 la inflexiunea suspecte.

Punctul O (0, 0) este un punct de inflexiune.

tot tabelul din proprietățile principale ale graficului pentru această funcție poate fi configurat numai pentru xÎ [0; + ¥), ca o consecință a simetriei centrale în ceea ce privește punctul grafic (0; 0):