Prezentarea pe care funcția dependența funcțională, sau funcția, este astfel

Prezentarea pe tema: „Care este funcția de dependență funcțională, sau funcția - aceasta este o astfel de relație între două variabile, în care fiecare valoare a variabilei independente ?.“ - Transcrierea:

1 Care este funcția? dependența sau funcția funcțională - este o astfel de relație între cele două variabile, în care fiecare valoare a variabilei independente corespunde la o valoare unică a variabilei dependente. Variabila independentă este, de asemenea, numit argumentul, dar dependent spun că aceasta este o funcție a argumentului. Toate valorile care sunt acceptate de variabila independentă, formează domeniul funcției.

2 Există mai multe modalități de definire a unei funcții: 1. Cu ajutorul mesei. 2.Grafichesky. 3.c folosind formule. Graficul unei funcții este mulțimea tuturor punctelor din planul de coordonate, care este egală cu valorile abscisei argumentului, și ordonata - valorile corespunzătoare ale funcției.

3

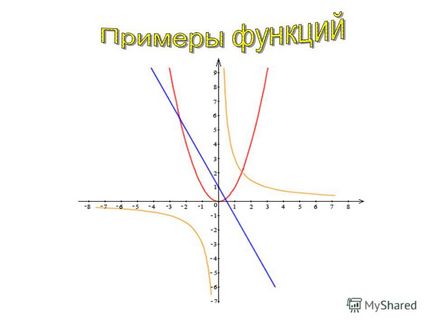
4 funcție liniară este o funcție care poate fi definită prin formula de forma y = kx + b, unde x - variabilă independentă, k și b - numerele dat. Pentru reprezentarea grafică funcția liniară este suficientă pentru a găsi coordonatele a două puncte ale graficului, nota aceste puncte în planul de coordonate și să aibă un drept prin intermediul lor. proporționalitate directă - funcție a formei y = kx, unde x - variabilă independentă, la - un număr de zero. Program de proporționalitate directă este o linie dreaptă care trece prin origine.

5 Construcția unui grafic funcție liniară pentru trasarea funcției lineare este necesar: - selectați oricare două valori ale lui x (argument), de exemplu, 0 și 1; - se calculează valoarea corespunzătoare a variabilei y (funcția). Rezultatele sunt înregistrate în tabelul y x01 convenabil - obținut punctele A și B descrie în sistemul de coordonate; - conectați linia de punctele A și B. Exemplu. Se trasează functia y liniar = -3 · x + 6. X01 y63

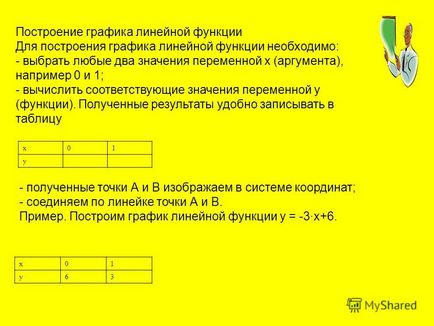
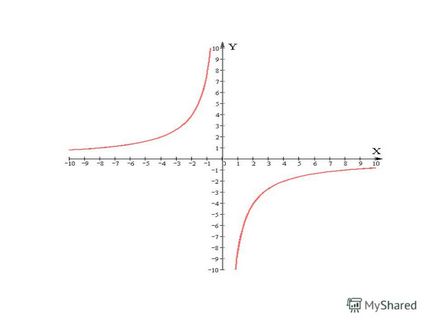
6 invers proporțională cu numita funcție, pe care o puteți seta tipul de formula la = k / x, unde x - variabilă independentă și k - un număr de zero. Domeniul acestei funcții este mulțimea tuturor celorlalte numere decât zero. Dacă valorile lui x și y sunt invers proporționale, relația funcțională dintre ele este exprimată prin ecuația y = k / x, unde k este o valoare constantă. Curba graficului inversă este compus din două ramuri. Acest grafic se numește hiperbolă. În funcție de semnul k ramuri ale unui hiperbolă sunt fie 1 sau 3 coordonate sferturi (k este pozitiv) sau în 2 și 4 coordonate sferturi (k este negativ). Figura prezintă un grafic al unei funcții y = k / x, unde k - este număr negativ.

7

0 deasupra axei OX; b „title =“ CAZURI SPECIALE funcție liniară. y = kx, k0, b = 0 - proporționalitate directă. Program - care trece prin linia de origine; y = b, k = 0, b0. . (B> 0, deasupra axei OX; b "class =" link_thumb „> 8 CAZURI SPECIALE funcție liniară y = kx, k0, b = 0 - proporționalitate Grafic directă - o linie dreaptă care trece prin origine ;. Y = b, k = 0, b0 (b> 0, deasupra axei OX ;. b 0, deasupra axei OX; b "> 0, deasupra axei OX; b"> 0, deasupra axei OX; b "title =" CAZURI SPECIALE funcție liniară y. = kx, k0, b = 0 - proporționalitate Grafic directă - o linie dreaptă care trece prin origine ;. y = b, k = 0, b0 (b> 0, deasupra axei OX; b „> 0, deasupra axei OX; b. . "title =" SPECIAL funcție CASES liniară y = kx, k0, b = 0 - directă proporționalitate Chart - o linie dreaptă care trece prin origine ;. y = b, k = 0, b0 (b> 0, deasupra axei OX. b „>

0k "title =" k> 0k "class =" link_thumb "> 9 k> 0k 0k"> 0k "> 0k" title = "k> 0k">

0k "title =" k> 0k „>

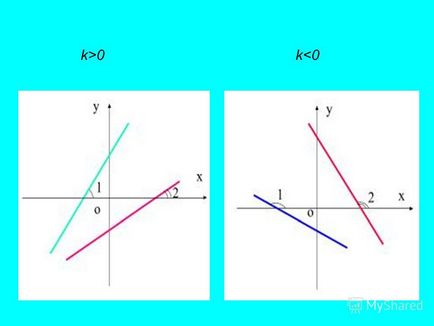
10 grafic dispunere reciprocă a unei funcții liniare. y = kx + b1, y = + b2 KX - grafice paralele. y = k1x + b, y = k2x + b - graficele se intersectează într-un punct (x; b).