Pregătirea studenților pentru examenul și OGE (DPA), în rezoluția centru de formare (manual de matematică -

Existența unui cerc înscris în triunghi

1. Determinarea bisectoarea unghiului se numește o grindă care împarte unghiul în două părți egale.

Teorema 1 (bisectoare proprietate principală). Fiecare punct de pe bisectoarea unghiului este aceeași distanță față de laturile unghiului (Fig.1).

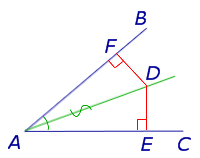
Dovada. D. Să considerăm un punct arbitrar situată pe bisectoarea unghiului BAC. și drop de la punctul D DE și DF perpendicularele la laturile unghiului (Fig.1). triunghiuri unghiulare ADE și ADF sunt egale. deoarece acestea sunt colțuri ascuțite DAF și DAE. și ipotenuzei AD - totală. Prin urmare,

QED.

Teorema 2 (inversa Teorema Teorema 1). Daca un punct este situat la aceeași distanță față de laturile unghiului. se afla pe bisectoarea unghiului (Figura 2).

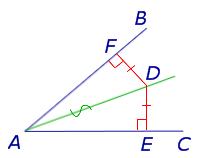
Dovada. Să considerăm un punct arbitrar D. situată în interiorul unghiului BAC și situate la aceeași distanță față de laturile unghiului. Picătură de la punctul D DE și DF perpendicularele la laturile unghiului (Figura 2). triunghiuri unghiulare ADE și ADF sunt egale. deoarece acestea sunt picioarele DF și DE. și ipotenuzei AD - totală. Prin urmare,

QED.

2. Determinarea cerc este unghiul cerc înscris. în cazul în care atinge laturile unghiului.

TEOREMA 3. Dacă cercul este înscrisă într-un unghi, distanța dintre punctele vertex de tangență la un cerc cu un unghi laturile egale.

Dovada. Lăsați punctul D - centrul cercului înscris în unghiul BAC. și punctele E și F - punct de cerc tangență cu laturi unghiulare (Figura 3).

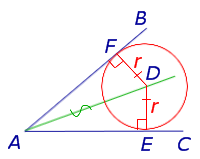
QED.

Notă. Teorema 3 poate fi, de asemenea, formulate într-un alt mod: segmente de tangente. transportate la circumferința unui punct, sunt egale.

3. Determinarea bisectoarea triunghi se numește un segment, care face parte din bisectoarea unghiului a triunghiului, iar triunghiul care unește vârful la un punct de pe partea opusă.

Teorema 4. În orice triunghi, toate cele trei bisectoare se intersectează la un moment dat.

Dovada. Luați în considerare două bisectoare efectuate de noduri A și C triunghi ABC. și reprezintă punctul de intersecție cu litera O (fig. 4).

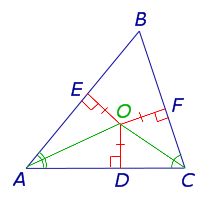
Picătură de la punctul perpendicularele O OD. OE și în partea laterală a triunghiului. Deoarece punctul O situată pe bisectoarea unghiului BAC. apoi prin Teorema 1 egalitatea:

Deoarece punctul O, situată pe bisectoarea unghiului ACB. apoi prin Teorema 1 egalitatea:

În consecință, egalitatea:

de unde, folosind Teorema 2 putem trage concluzia că O se află pe bisectoarea unghiului ABC. Astfel, toate bisector trei triunghi trece prin același punct, după cum este necesar

4. Definirea unui cerc înscris într-un triunghi. Este cercul care atinge toate laturile triunghiului (Figura 5). În acest caz, triunghiul se numește un triunghi, un cerc descris despre.

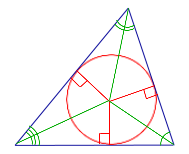
Corolar. În orice cerc triunghi poate fi înscris, și numai unul. Centrul unui cerc înscris în triunghiul este punctul în care se intersectează toate Bisectoarele unui triunghi.

Formula pentru raza unui cerc înscris în triunghi

Formula vă permite să găsiți raza unui cerc înscris în triunghiul. convenabil reprezentată în tabelul următor.