Patrulater cu unghiuri drepte - l

Una dintre cele mai interesante subiecte din geometria anului școlar - este „un patrulater“ (clasa 8). Ce tipuri de figuri există, ce calități speciale le posedă? Ceea ce este unic despre patrulatere cu unghiuri de nouăzeci de grade? Să ne uităm la toate astea.

Ce figură geometrică numit patrulater

Poligoane care constau din patru laturi, respectiv, ale celor patru noduri (colturile) sunt numite în patrulatere geometrie euclidiene.

Interesat de istoria acestui tip de cifre nume. în română noun „patrulater“ este derivat din expresiile „patru colțuri“ (în același mod ca „triunghiul“ - cele trei unghiuri, „pentagon“ - cinci unghiuri, etc ...).

Cu toate acestea, în limba latină (care a venit prin intermediul multor termeni geometrice în cele mai multe limbi ale lumii), este numit un patrulater. Acest cuvânt este un Quadri numeral (patru) și o latus Substantiv (lateral). Deci, putem concluziona că acest vechi poligon a fost cunoscut doar ca „patrulater“.

Apropo, numele (cu accent pe prezența cifrelor de acest tip de patru laturi, nu colțuri) reținute în unele limbi moderne. De exemplu, în limba engleză - patrulater și în franceză - quadrilatère.

În cele mai multe limbi slave această specie este identificată cifrele în continuare cu privire la numărul de colțuri, nu laturile. De exemplu, în limba slovacă (štvoruholník), în limbile bulgară ( „chetiriglnik "), în Belarus (" chatyrohkutnіk ") în limba ucraineană (" chotirikutnik„), în Cehia (čtyřúhelník), dar în patrulaterul polonez a făcut apel la numărul de partide - czworoboczny.

Ce tipuri de quad-uri de a fi studiate în programa școlară

În geometria modernă sunt 4 tipuri de poligoane cu patru laturi.

Cu toate acestea, datorită proprietăților foarte complexe ale unora dintre ele pe clase de geometrie de școală sunt familiarizați doar cu două feluri.

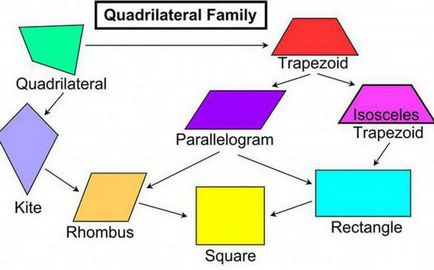
• Paralelogram (paralelogram). Opozante laturile patrulaterului sunt paralele între ele și, respectiv, sunt egale în perechi.
• Trapezoid (trapez sau trapezoidală). Acest patrulater este format din două laturi opuse paralele între ele. Cu toate acestea, cealaltă pereche de laturi nu are nici o astfel de facilitate.

Nu a fost studiat în cadrul școlii de tipuri de geometrie patrulatere

În plus față de acestea, există două tipuri de patrulatere cu care elevii nu sunt familiarizați cu lecții de geometrie, din cauza complexității lor speciale.

• Deltoid (zmeu) - figura, în care fiecare dintre cele două perechi de laturi adiacente egale în lungime între ele. Numele acestui patrulater sa datorat faptului că, în aparență el este destul de amintește de literă a alfabetului grecesc - „Delta“.
• Paralelogram (isoscel) - această cifră este la fel de complex ca și numele său. În ea cele două părți opuse sunt egale, dar ele nu sunt paralele între ele. Mai mult decât atât, laturile lungi opuse ale patrulaterului intersectează celelalte două laturi mai scurte continuare.

tipuri de paralelogram

Având în tratate cu principalele tipuri de quad-uri, ar trebui să acorde o atenție la subspecie. Deci, toate paralelograme, la rândul lor, sunt de asemenea împărțite în patru grupe.

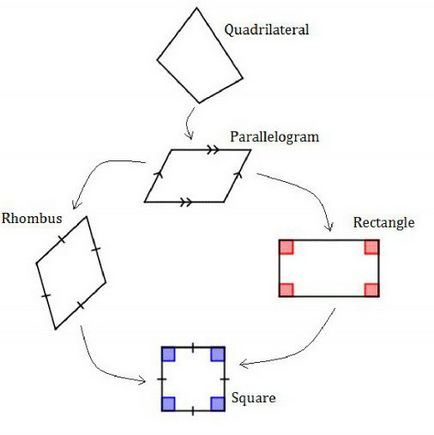
• paralelogram Classic.
• Rhombus (romburi) - forma de patrulater cu laturile egale. diagonalele sale se intersectează în unghi drept, împărțind rombul în patru triunghiuri egale în unghi-dreapta.
• Dreptunghi (dreptunghi). Acest nume vorbește de la sine. Din moment ce acest dreptunghi cu unghiuri drepte (fiecare dintre ele egal cu nouăzeci de grade). laturile opuse nu numai paralele între ele, dar egal.
• Pătrat (pătrat). Deoarece dreptunghi este un patrulater cu unghiuri drepte, dar el are toate laturile egale. Acest lucru, această cifră este aproape de un diamant. Deci, se poate argumenta că pătrat - este o încrucișare între un diamant și un dreptunghi.

Proprietățile speciale ale dreptunghiului

Având în vedere cifrele, în care fiecare dintre colțurile dintre părți este egală cu nouăzeci de grade, este în valoare de un accent mai aproape pe dreptunghi. Deci, ce caracteristici are caracteristici care îl diferențiază de alte paralelogram?

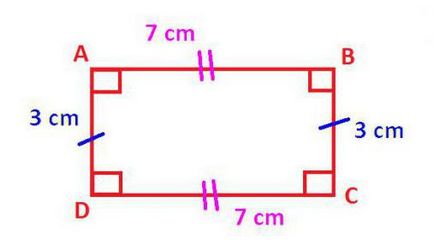
Pentru a afirma că paralelogramului subiect - un dreptunghi, diagonalele sale trebuie să fie egală cu unul pe altul, și fiecare dintre colțuri - drepte. În plus, pătratul diagonalele sale trebuie să îndeplinească suma pătratelor celor două laturi adiacente ale figurii. Cu alte cuvinte, dreptunghiul clasic este format din două triunghiuri unghi drept, așa cum sunt ele cunoscute, suma pătratelor picioarelor este egală cu pătratul ipotenuzei. În rolul ipotenuzei servește diagonală patrulaterul luate în considerare.

Ultima dintre aceste semne de această cifră este, de asemenea, proprietatea sa specială. În plus, există și altele. De exemplu, faptul că toate părțile studiate patrulater cu unghiuri drepte - este atât de înălțimea sa.

Mai mult decât atât, în cazul în care un dreptunghi în jurul fiecărui desena un cerc, diametrul său va fi egală cu diagonala formelor inscriptionate.

Printre alte proprietăți ale patrulaterului, faptul că acesta este plat și geometria non-euclidiene nu există. Acest lucru se datorează faptului că într-un astfel de sistem nu există nici o figura patrulateră, suma unghiurilor este egală cu trei sute șaizeci de grade.

Pătratul și caracteristicile sale

Având în tratate cu caracteristicile și proprietățile dreptunghiului, ar trebui să acorde o atenție la al doilea cunoscut patrulaterul știință, cu unghiuri drepte (un pătrat).

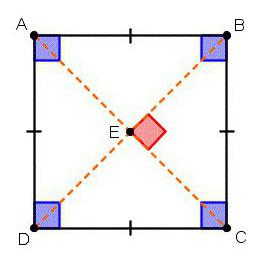
Ca și în fapt același dreptunghi, dar cu laturile egale, această formă are toate proprietățile sale. Dar, spre deosebire de el, piața este prezent în geometria non-euclidiene.

În plus, în această figură, există alte caracteristici individuale. De exemplu, faptul că diagonala unui pătrat nu este pur și simplu egal între ele, dar se intersectează în unghiuri drepte. Astfel, ca un romb, un pătrat format din patru triunghiuri unghi drept, care este împărțit în diagonală.

În plus, această cifră este cea mai echilibrată a tuturor dreptunghiuri.

Care este suma unghiurilor unui patrulater

Având în vedere caracteristicile dreptunghiuri ale geometriei euclidiene, ar trebui să acorde o atenție la colțurile lor.

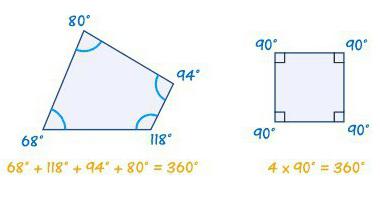
Astfel, în fiecare din cifrele de mai sus, indiferent dacă există în unghiuri drepte ei sau nu, valoarea totală a acestora este întotdeauna același - trei sute șaizeci de grade. Aceasta este o caracteristică unică a acestui tip de cifre.

patrulatere perimetrale

După ce a ocupat de asta, ceea ce este suma unghiurilor unui patrulater și alte proprietăți speciale ale formei de acest fel, este necesar să se cunoască ce este cel mai bine să utilizeze formule pentru a calcula perimetrul și zona lor.

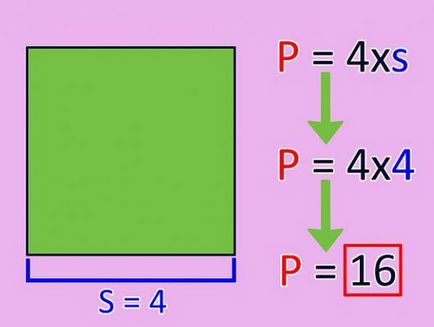
Pentru a determina perimetrul oricărui patrulater, trebuie să adăugați numai până la unul pe altul lungimea laturilor sale.

De exemplu, în figura klmn circumferința sa poate fi calculată cu formula: P = KL + LM + MN + KN. Dacă înlocuim aici numerele obținute: 6 + 8 + 6 + 8 = 28 (cm).

În cazul în care cifra considerată - un pătrat sau un romburi, pentru găsirea perimetrului formulei poate fi simplificată prin simpla înmulțirea lungimii uneia dintre laturile sale cu patru P x = KL exemplul 4. 6 x 4 = 24 (cm).

Formula dreptunghiuri pătrat

După ce a ocupat de modul de a găsi perimetrul de orice formă, cu patru colțuri și părți ar trebui să ia în considerare cele mai populare și ușor mod de a găsi zona ei.

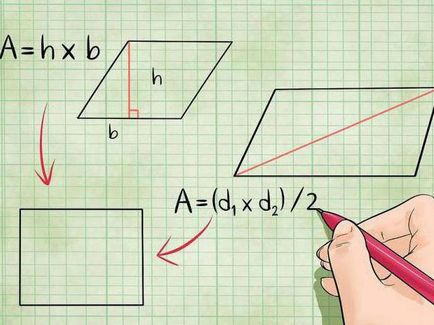
• Modul clasic de a calcula - este de a folosi formula S = 1/2 x LN KM x SIN LON. Se pare că orice zonă a patrulaterului este egală cu jumătate din produsul diagonalelor pe sinusul unghiului situat între ele.
• În cazul în care cifra a cărei suprafață trebuie să găsească - este un dreptunghi sau pătrat (a cărui diagonală este întotdeauna egală între ele), putem simplifica formula, ridicat în pătratul lungimii de o diagonală și înmulțirea cu sinusul unghiului dintre ele și împărțirea în jumătate toate. De exemplu: S = 1/2 CM 2 x SIN LON.
• De asemenea, în cazul în care aria unui dreptunghi poate ajuta în jurul perimetrului considerat cifre și lungimea uneia dintre laturile sale. Într-un astfel de caz, va fi mai ușor să se folosească formula S = KN x (P - 2 KN) / 2.
  
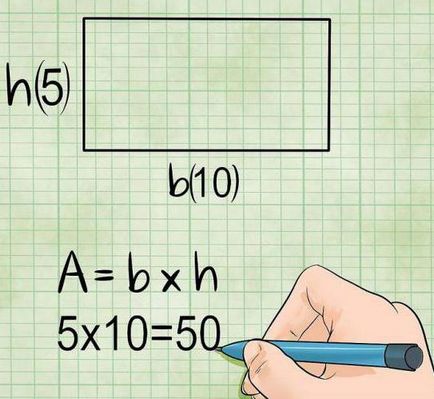
• În cazul pătratului proprietăților sale permit utilizarea mai multor formule suplimentare pentru a găsi zona. De exemplu, cunoscând formele perimetrale pot fi utilizate astfel de variantă: S = P 2 / 16. Și dacă cunoscută raza cercului înscris într-un patrulater, o zonă de pătrat este cale foarte similară: S = 4r 2. Dacă raza cercului este cunoscută, apoi altă formulă adecvată: S = 2R 2. de asemenea, zona de pătrat este egală cu 0,8 linie lungă trase din colțul figurii la mijlocul laturii opuse.
• În plus față de toate cele de mai sus, există, de asemenea, o formulă separată pentru a găsi zona, conceput special pentru paralelogramului. Acesta poate fi utilizat, dacă este cunoscută, lungimea celor două înălțimi ale figurii și mărimea unghiului dintre ele. Apoi, înălțimea să fie multiplicată între ele și sinusul unghiului dintre ele. Este demn de remarcat faptul că puteți utiliza această formulă pentru toate cifrele, care se referă la paralelograme (de exemplu, dreptunghi, romb și pătrat).

Alte proprietăți patrulatere: cercuri inscriptionare circumscrise

Luând în considerare caracteristicile și proprietățile unui patrulater ca forma geometriei euclidiene, este în valoare de atenție la posibilitatea de a descrie runda sau intră în interiorul următoarele:

• În cazul în care suma unghiurilor opuse ale unei calculezi de o sută optzeci de grade și sunt egale una de alta, este posibil să se descrie un cerc în mod liber în jurul acestui patrulater.
• Conform teoremei lui Ptolemeu, dacă cercul descris în afara poligon cu patru laturi, produsul diagonalelor este egal cu suma produselor din laturile opuse ale figurii. Astfel, formula ar fi: CM x LN = KL x MN + LM x KN.
• Dacă vă construi un dreptunghi în care suma laturile opuse sunt egale una de alta, atunci este posibil să se înscrie într-un cerc.

Având în tratate cu faptul că un astfel de patrulater, pentru care există tipuri de ea, care dintre ele au doar unghiuri drepte între părți și ce proprietăți care le au, ar trebui să ne amintim toate aceste lucruri. În formula special găsirea perimetrului și zona poligoanelor considerate. La urma urmei, cifra acestei forme - una dintre cele mai comune, iar această cunoaștere poate fi util pentru calcule în viața reală.