Matematica pentru blonde diagonala unui paralelipiped

Asta mi sa pus o întrebare interesantă: cum să găsească volumul unui paralelipiped, cunoscând sale trei diagonalele care merg de la un vârf? Primul meu gând - să sape în manualul matematic. Dar de referință meu preferat este tăcut. Există un alt izvor de înțelepciune - Wikipedia. Pagina de limbă rusă pe paralelipipedic impresionează prin mizeria ei. Teorema lui Pitagora Chiar și pentru spațiul tridimensional nu este acolo. De obicei, în astfel de cazuri, am rândul său, pe aceeași pagină exact în limba engleză. La urma urmei, matematica - este genul de lucru care nu are nevoie de traducători. Cel mai adesea, există mult mai multe formule diferite. În acest moment am fost de așteptare pentru o mare dezamăgire. Da, am văzut acolo teorema lui Pitagora pentru a cuboidului. Și totuși. Orice gunoi matematic în vrac Wikipedia, dar cel mai interesant acolo. Pechalka.

Să încercăm să gândim logic. Dacă cineva a fost întrebat o astfel de problemă, atunci soluția la această problemă este. matematica noastre nu au ajuns încă la scadență, până la punctul în care elevii săi a recunoscut ignoranța lui de ceva. Este că cei mai indrazneti. Restul prostește repeta ceea ce a fost o dată le-a învățat. Acest lucru sugerează soluția: compila teorema lui Pitagora la trei muchii diagonale, să le combine într-un sistem de trei ecuații cu trei necunoscute, rezolva și de a găsi dimensiunile unui paralelipiped. Brrrr! Horror.

Acum ne gândim pe cealaltă parte. Volum - rezultatul înmulțirii lungimii de trei măsurători. Avem trei lungime diagonală. Teoretic, se poate obține suma. Să atragă diagonala noastră a unui cuboid, și să vedem ce putem face cu ele. Uită-te din unghiuri diferite, pentru a face clar.

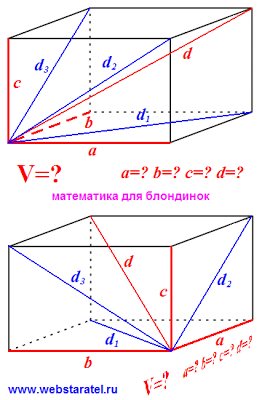
In imagine este evidențiată în paralelipipedic albastru acele elemente care sunt cunoscute la noi. Aceste margini diagonale. Roșu a subliniat faptul că noi nu știm. Este diagonala unui paralelipiped dreptunghic, iar dimensiunile sale liniare (cum ar fi matematica încă le numim dimensiunile cutiei). Oh, și volumul mare de noi este, de asemenea, nu este cunoscut.

Acum, înarmat cu vechi bunicul teorema lui Pitagora și scrie dimensiunile formulă și diagonalele. O cutie avem o formă dreptunghiulară, atunci toate unghiurile dintre dimensiunile liniare și marginile drepte. Nu uităm că obiectivul nostru principal - pentru a găsi volumul.

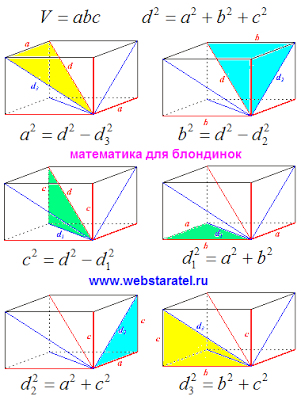
Imagini de la mai multe formule distrage atenția. Scriem formula heap separat. Matematica, în acest caz, cu înțelepciune vorbit cu „o mulțime de formule matematice.“ Ne uităm la formula și să încerce să cel puțin ceva să se gândească. Trebuie să scăpăm de măsurare și diagonala unui paralelipiped dreptunghiular, deoarece acestea nu sunt cunoscute la noi. Acum, dacă diagonala a cutiei exprimată în ceea ce privește fețele laterale diagonale. Foarte mult formulă în jumătatea dreaptă a unui pumn de similar cu unul de altul.

Acolo! Diagonală de fețele pătrate sunt două pătrate pe diagonală caseta. Acum, pur și simplu. Ca blocuri în grădiniță. Eliminați paranteze, adăugați paranteze. Și vom obține formula.

După aceea, formula care rezultă este substituit în formula cu dimensiunile liniare și obține dimensiunile liniare de expresie prin fețele diagonale. Apoi înregistrăm volumul de formula.

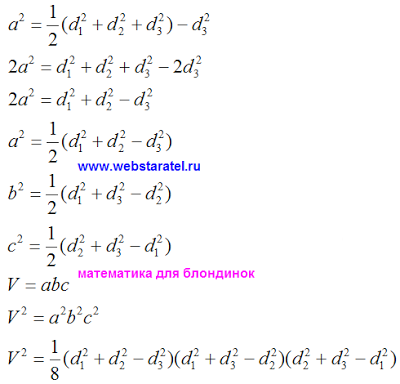
Totul. Problema este rezolvată. Rezultatul a fost o formulă foarte frumos și elegant. Suma pătratelor celor două diagonale ale fețelor pătrat scade a treia fata. Apoi este multiplicat, împărțit în opt ture de volum, ale unui paralelipiped la pătrat. Am înțeles că aceasta este una dintre proprietățile fundamentale ale spațiului. Folosind principiul rearanjare și cofactori termeni pot fi afișate formule similare pentru spații multidimensionale cu orice număr de dimensiuni. Orice volum multivariate poate fi exprimată în termenii elementelor cu un număr mai mic de măsurători. Din păcate, vom face acest lucru matematica pe care nu-i spune nimic. Ori ei nu știu nimic, sau timid. Dar, lipsit de orice probleme, care sunt atât de mândru de profesorii noștri în fața noastră frumusețea matematicii în forma sa originală.