funcţia Program

Graficul functiei.

Am ales dreptunghiular planul sistemului de coordonate și am complot valoarea abscisa a argumentului x. iar axa ordonatei - valoarea funcției y = f (x).

Graficul funcției y = f (x) este multimea tuturor punctelor ale căror absciselor aparțin domeniului funcției, iar valorile ordonatelor sunt egale cu funcția corespunzătoare.

Cu alte cuvinte, graficul funcției y = f (x) - este multimea tuturor punctelor din planul, coordonatele x, y satisfac relația y = f (x).

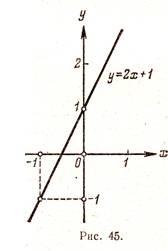
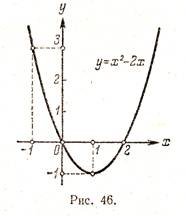
Fig. 45 și 46 prezintă graficele 2x + y = 1 și y = x 2 - 2x.

Strict vorbind, ar trebui să se facă distincția între graficul funcției (o definiție matematică precisă, care a fost prezentată mai sus) și tras de o curbă, care dă întotdeauna o schiță mai mult sau mai puțin precisă a graficului (și chiar și atunci, de regulă, nu doar grafica, dar numai o parte din ea se află în finală porțiune plană). În viitor, cu toate acestea, vom spune de obicei „program“ și nu „grafica schiță.“

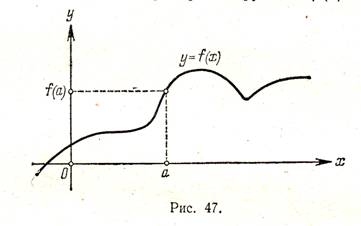
Cu programul, puteți găsi valoarea funcției în punctul. Și anume, în cazul în care punctul x = a în domeniul funcției y = f (x). apoi pentru determinarea numărului de f (a) (m. f. valori ale funcției de la x = a) ar trebui să facă acest lucru. Necesitatea de prin punctul cu abscisa x = a desena o linie dreaptă paralelă cu axa y; această linie intersectează graficul unei funcții y = f (x) la un moment dat; ordonata a acestui punct va fi, prin definiție, grafică egală cu f (a) (Fig. 47).

De exemplu, pentru o funcție f (x) = x 2 - 2x prin grafică (. Figura 46) obținem f (-1) = 3, f (0) = 0, f (1) = -l, f (2) = 0 și t. d.

grafic Funcția ilustrează comportamentul și proprietățile funcției. De exemplu, din Fig. 46 este clar că funcția y = x 2 - 2x ia valori pozitive pentru x <0 и при х> 2. negativ - la 0

Pentru a construi graficul funcției f (x) pentru a găsi toate punctele planului, coordonatele x, y care satisfac ecuația y = f (x). În cele mai multe cazuri, acest lucru nu este posibil, deoarece un astfel de număr infinit de puncte. Prin urmare, graficul de aproximativ descrie - cu o precizie mai mare sau mai mică. Cea mai simplă metodă este reprezentarea grafică de mai multe puncte. Acesta constă în faptul că argumentul x dă un număr finit de valori - să zicem, x1. x2. x3. XK și se completează până masă, care include valoarea funcției selectate.

Tabelul după cum urmează:

Cele cinci puncte corespunzătoare sunt prezentate în Fig. 48.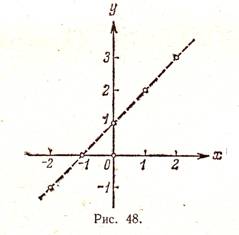

Bazat pe localizarea acestor puncte, se concluzionează că graficul funcției este o linie dreaptă (prezentată în Fig. 48 în fantomă). Putem lua în considerare această concluzie este de încredere? Dacă nu argumente suplimentare pentru a susține această concluzie, poate fi cu greu considerate fiabile. de încredere.

Pentru a susține teza, ia în considerare funcția

Calculele arată că valorile acestei funcții la punctele -2, -1, 0, 1, 2 descris mai sus tabelul de mai sus. Cu toate acestea, graficul acestei funcții nu este o linie dreaptă (prezentată în fig. 49). Un alt exemplu este functia y = x + l + sinπx; valoarea sa este de asemenea descrisă în tabelul de mai sus.

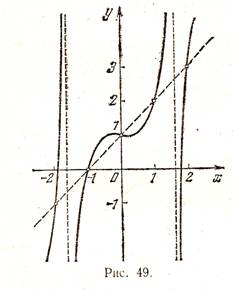
Aceste exemple arată că metoda formă „pură“ complot mai multe puncte nesigure. Prin urmare, pentru a construi un anumit grafic funcție, în general, se procedează după cum urmează. La început, studiind proprietățile acestei funcții, cu care se poate construi o schiță de program. Apoi, calcularea valorilor funcției la mai multe puncte (alegerea cărora depinde de proprietățile setului funcției) sunt generate punctul corespunzător. În cele din urmă, prin intermediul punctelor reprezentate grafic se realizează curba, folosind proprietățile funcției.

Unele (cele mai simple și mai frecvent utilizate) proprietățile funcțiilor utilizate pentru identificarea schiță grafică, ne vom uita la mai târziu, dar examina acum câteva metode utilizate în mod obișnuit de diagrame.

Graful y = | f (x) |.

Unul construi adesea graficul functiei y = | f (x) |, unde f (x) - o anumită funcție. Să ne amintim cum se face. Prin definiție, valoarea absolută a numărului poate fi scris

Aceasta înseamnă că graficul y = | f (x) | pot fi obținute din grafic, funcția y = f (x) după cum urmează: toate punctele graficului funcției y = f (x). a căror ordonator non-negativ, trebuie admis; Mai mult, în loc de graficul punctelor y = f (x). având coordonatele negative, trebuie să construiască punctul corespunzător de pe graficul funcției y = -f (x) (m. e. o parte din graficul functiei
y = f (x). care se află sub axa x, ar trebui să se reflecte în mod simetric față de axa x).

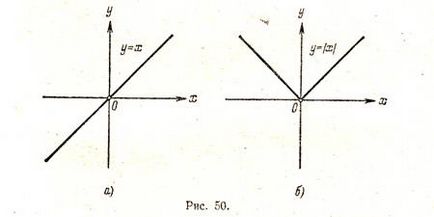
Exemplul 2. Construirea unui grafic al y = | x |.

Luam graficul functiei y = x (Fig. 50 a) și o parte a graficului la x <0 (лежащую под осью х ) симметрично отражаем относительно оси х. В результате мы и получаем график функции у = |х| (рис. 50, б).

Exemplul 3. Se trasează funcția y = | x 2 - 2x |.

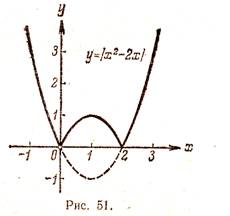
În primul rând, vom construi un grafic al unei funcții y = x 2 - 2x. Graficul acestei funcții - Ramurile parabole care sunt îndreptate în sus, vârful parabolei are coordonatele (1, -1), graficul acesteia intersectează axa x la punctele 0 și 2. În intervalul (0, 2) fuktsii ia valori negative, astfel încât această parte a graficului se va reflecta în mod simetric în raport cu abscisa. In Figura 51 am complot functia y = | x 2 -2x |. bazat pe graficul funcției y = x 2 - 2x

Graful y = f (x) + g (x)

Luați în considerare problema construirii graficului y = f (x) + g (x). cu excepția cazului în funcțiile grafice specificate y = f (x) și y = g (x).

Rețineți că domeniul funcției y = | f (x) + g (x) | Este setul de acele valori x pentru care au determinat funcția atât y = f

Să presupunem că punctele (x0. Y1) și (x0. Y2), respectiv, aparțin funcțiilor grafic y = f și y = g (x). t. e. y1 = f (x0), y2 = g (x0). Apoi, punctul (x0;. Y1 + y2) apartine graficului y = f (x) + g (x) (pentru f (x0) + g (x0) = y1 + y2). în orice punct al graficului y = f (x) + g (x) pot fi obținute prin aceasta. În consecință, graficul funcției y = f (x) + g (x) pot fi obținute din graficele y = f (x). și y = g (x) prin înlocuirea fiecărui punct (xn. y1) graficul y = f (x) punctul (xn. y1 + y2), unde y2 = g (xn), m. e. deplasa fiecare punct (xn. y1) a graficului y = f (x) în lungul axei y cu valoarea y1 = g (xn). Aici vom considera numai acele puncte xn determinate pentru care atât funcția y = f (x) și y = g (x).

O astfel reprezentarea grafică a funcției y = f (x) + g (x) se numește metoda prin adăugarea graficelor y = f (x) și y = g (x)

Exemplul 4. în figură prin adăugarea graficelor reprezentate grafic funcție
y = x + sinx.

În construcția graficului y = x + sinx, am presupus că f (x) = x și g (x) = sinx. Pentru a construi graficul va selecta un punct cu abtsissami -1,5π, -, -0,5, 0, 0,5, 1,5, 2. Valorile lui f (x) = x, g (x) = sinx, y = x + sinx calculeaza la punctele selectate, iar rezultatele sunt puse într-un tabel.