Elasticitatea funcției - studopediya

Instrumente financiare derivate de ordin superior

Deoarece derivata funcției în sine este o funcție, aceasta poate fi, de asemenea, derivate. Conceptul de derivat, care a fost discutat mai sus, se referă la un derivat al primului ordin.

Derivata de ordinul n-lea este derivata derivatului
(N - 1) comanda -lea. De exemplu, f `` (x) = (f `(x))` - derivata de ordinul doi (sau al doilea derivat), f `` `(x) = (f`` (x)) `- derivata treilea ordin (sau al treilea derivat), etc. Uneori, pentru a denota derivați de ordin superior sunt utilizate romane sau cifre arabe în paranteze, de exemplu, f (5) (x) sau f (V) (x) pentru derivatul cincea comandă.

Semnificația fizică a derivatelor de ordin superior definite în același mod ca și pentru primul derivat: fiecare dintre ele reprezintă o rată de derivat modificarea ordinii anterioare. De exemplu, derivata a doua este rata de schimbare a primului, adică Rata de viteză. Pentru mișcarea rectilinie este punctul de accelerare în timp.

Funcția Elasticitate Ex (y) se numește limita raportul sporului relativ al funcției, la o creștere relativă a argumentului x, ultimul tinde la zero :.

Funcția Elasticitate arată cu aproximație, funcția variație procentuală y = f (x) cu x modificări variabile independente cu 1%.

Din punct de vedere economic, diferența dintre acest indice pe derivatul că derivatul are unitățile de măsură și, prin urmare, valoarea sa depinde de unitățile în care variabila măsurată. De exemplu, în cazul în care dependența producției pe cantitatea de timp este exprimat în tone, respectiv, și luni, instrumentul derivat va arăta creșterea limitei în tone pe lună; în cazul în care măsura acești indicatori, de exemplu, în kilograme, și zile, și funcția în sine și derivatul său va fi diferit. Flexibilitatea este, de asemenea, în mod inerent cantitate adimensional (măsurată în procente sau fracțiuni) și, prin urmare, nu depinde de amploarea ratelor.

teoreme de bază asupra funcțiilor diferențiabile și aplicațiile lor

Teorema lui Fermat. Dacă funcția diferențiabilă interval atinge cea mai mare sau cea mai mică valoare din punctul intern al deschiderii, derivata funcției în acest moment este zero.

Sensul geometric al teoremei constă în faptul că la punctul de cea mai mare sau cel puțin o valoare atinsă în interiorul intervalului, tangenta este paralelă cu graficul abscisa (Figura 3.3).

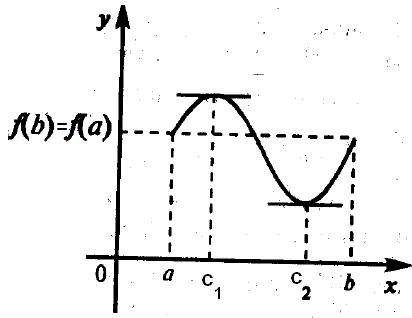
Teorema lui Rolle. Lăsați funcția y = f (x) îndeplinește următoarele condiții:

1) continuă pe intervalul [a, b];

2) este diferențiabilă la interval] a, b [;

3) la punctele finale cu valori egale, adică, f (a) = f (b).

Apoi, în cadrul segmentului există cel puțin un punct la care funcția derivat este zero.

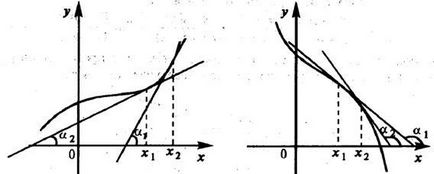
Sensul geometric Teorema Rolle este că există cel puțin un punct în care tangenta la graficul de axa x este paralelă cu (de exemplu, în figura 3.4 două astfel de puncte).

Dacă f (a) = f (b) = 0, Rolle teorema poate afirma într-un alt mod, între două zerouri succesive funcție diferențiabilă are cel puțin un zero al derivatului.

Teorema lui Rolle este un caz particular al teoremei lui Lagrange.

Teorema lui Lagrange. Să presupunem că funcția y = f (x) îndeplinește următoarele condiții:

1) continuă pe intervalul [a, b];

2) este diferențiabilă la intervalul (a, b).

Apoi, în interiorul segmentului există cel puțin un astfel de punct, cu, în derivatul kdtoroy este egal cu raportul dintre incrementul funcției pe incrementul argumentului pe acest segment :.

Pentru a înțelege semnificația fizică a teoremei lui Lagrange, observăm că nu este nimic mai mult decât rata medie a funcției de schimbare pe intervalul [a, b]. Astfel, teorema spune că în cadrul segmentului există cel puțin un punct în care rata „instantanee“ de schimbare a funcției este egală cu rata medie de schimbare în întregul segment.

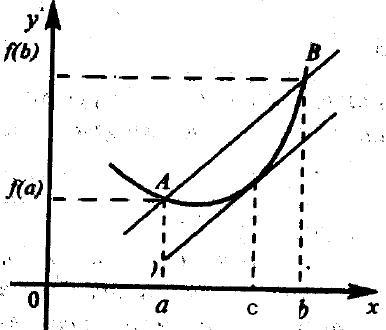
Semnificația geometrică a teoremei lui Lagrange este ilustrată figura 3.5. Rețineți că expresia este o pantă a liniei, pe care se află coarda AB. Teorema afirmă că funcția graficului, există cel puțin un punct în care tangenta la aceasta este paralelă cu această coardă (adică, panta tangentei - derivata - va fi la fel).

Consecință: dacă derivatul este zero la un anumit interval de timp, atunci funcția identic constantă pe acest interval.

De fapt, să ia pe acest interval [a, b] interval [a, x]. Prin teorema lui Lagrange în acest interval există un punct cu, pentru care. Prin urmare f (a) - f (x) = f '(a) (a - x) = 0; f (x) = f (a) = const.

regula L'Hospital lui. Limita raportului dintre două funcții infinit mici sau infinit mari este egală cu limita raportului dintre derivații lor (finită sau infinit), în cazul în care acesta din urmă există în acest sens.

Cu alte cuvinte, în cazul în care există o incertitudine a formei, atunci.

Aplicarea regula L'Hopital pentru a găsi limita va fi revizuită în clase practice.

O condiție suficientă pentru creșterea funcției (descreștere). Dacă pozitiv funcția derivat diferențiabilă (negativ) într-o anumită perioadă de timp, atunci crește funcție (descrește) în acest interval.

Dovada. Luați în considerare x1 două valori și x2 dintr-un anumit interval de timp (să zicem, x2> x1). Prin Teorema LaGrand pe [x1. x2] există un punct de unde. De aici f (x2) - f (x1) = f '(c) (x2 - x1). Apoi, pentru f `(c)> 0, în partea stângă a inegalității este pozitiv, adică, f (x2)> f (x1), iar funcția este în creștere. Când f `(c) <0 левая часть неравенства отрицательна, т.е. f(х2 )

Funcția de interpretare geometrică condiții monotonie: în cazul în care tangenta la curba la un anumit interval sunt orientate în unghi ascuțit față de axa orizontală, crește funcții, iar dacă la obtuz scade apoi (vezi Figura 3.6.).

Notă: Condiția prealabilă pentru monotonia mai slabi. Dacă crește funcție (scade), la un anumit interval de timp, atunci derivatul este non-negativ (non-pozitiv), în acest interval (adică, la puncte separate, funcțiile monotone derivate pot fi zero).