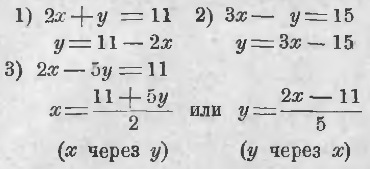Ecuațiile de gradul I cu două necunoscute matematică

55. Ecuația cu două necunoscute. Acum ia în considerare ecuația

Este sarcina înregistrării: găsi valorile numerice pentru x și y, la binomială 5x + 3y sa dovedit egal cu numărul 18.

Știm că în cazul în care două termenul-ar fi doar un număr necunoscut, și chiar și atunci am fost capabili să rezolve ecuația corespunzătoare. Prin urmare, există o considerație faptul că este una dintre necunoscutele este cum să fie de prisos: dacă în loc de y necunoscut, de exemplu, pentru a lua unele număr, obținem o ecuație cu o singură necunoscută.

Și dacă da, atunci această ecuație ar trebui să aibă o mulțime de soluții, și se pare că metoda lor de preparare, Să ne dea una dintre necunoscutele, de exemplu, y, și valori arbitrare ori de câte ori obținute din ecuația 1 pentru a determina necunoscutul va deveni un alt x necunoscut. Pentru a face acest lucru mai multă ordine, va rezultatele record în tabel.

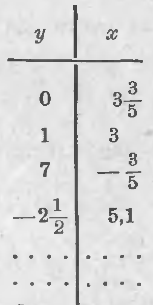
Dăm acum y este 0, t. E., presupunem că y = 0 (scris în prima linie a tabelului). Atunci ecuația noastră va aborda în

(Înregistrare Tabelul acest număr în coloana a doua, intitulată literelor x).

Deci avem o singură soluție a ecuației: y = 0 și x = 3 (3/5) (în cazul în care aceste valori sunt substituite în nostru binom în loc de x și y, cerința ca binomială egal cu numărul 18, este justificată:
3 * 3 (3/5) + 3 * 0 = 18).

Ne da o valoare y 1, adică, presupunem că y = 1 (a doua linie a tabelului) ..; atunci vom obține

de la 5x = 18 - 3 sau 5x = 15 și x = 3 (înregistrată în linia a 2-a). Așa că am găsit a doua soluție a ecuației y = 1 și x = 3.

Noi acum da y valoarea 7, adică, presupunem că y = 7 ..; atunci obținem 5x ecuație + 21 = 18, unde 5x = -3 și x = -3/5 (vezi. al treilea rând al tabelului).

Să presupunem = încă y -2½; apoi 5x + 3 (-2½) = 18 sau 5x - 7½ = 18 unde 5x = 25½ și x = 5 (1/10) = 5.1 (vezi patra linie a tabelului.). Acest lucru poate fi extins în măsura în care se dorește. Deci, o ecuație cu două necunoscute are infinit mai multe soluții; pentru a le obține este necesar să se dea unul un valori necunoscute și arbitrare ale ecuațiilor rezultate pentru a determina de fiecare dată un alt necunoscut.

. Având în vedere tabelul anterior, și reamintind punctul 49, vom stabili: am fost variabile independente y, x - dependente, sau este o funcție de x y - o.

Putem accelera oarecum la activitatea de a găsi soluții la această ecuație. y numerotată pentru un anumit număr de (în continuare, la urma urmei, y de fiecare dată când am înlocuit un număr cunoscut); apoi pe ecuația 5x + 3y = 18, putem vedea cum o ecuație cu un x necunoscut și de a rezolva această ecuație:

5x = 18 - 3y; x = (18 - 3y) / 5

Ne putem exprima în cuvinte acest rezultat pentru că am identificat în această ecuație y prin x.

Acum, în conformitate cu formula (18 - 3y) / 5, putem găsi cu ușurință o mulțime de soluții, ceea ce face calcule în minte. Să presupunem, de exemplu, y = 2. Apoi este necesară (3) înmulțit cu (2), obținem -6; fold (18) și (-6) - obține 12 și împărțit în 5 - obține x = 2 (2/5). Mai lasa y = 10; apoi (-3) + (10) = -30; (+18) + (-30) = -12; (-12). (+5) = -2 (2/5), t. E. X = -2 (2/5) și t. D.

Să luăm ecuația:

Noi luăm pentru variabila x independentă, în timp ce dependența de y y și este definit de x. Acest lucru se poate face prin două metode:

Acesta poate fi mai convenabil la primirea a doua 1, deoarece punerea sa în aplicare este mai ușor de imaginație, în cazul în care este de dorit să se efectueze determinarea y-x și în minte.

Acum putem găsi orice număr de soluții ale ecuației: 1) x = 0; y = -5 (2/3); 2) x = 1; y = -4; 3) x = -1; y = -7 (1/3) și t. d.

Este necesar să se obișnuiască rapid (în mintea mea) pentru a defini una dintre necunoscutele ecuației cu două necunoscute printr-un alt. exemple:
f55_3