Determinarea patrulaterul

Lecții de focalizare

Obiective lecție

• Educațional - repetiție, sinteza și testarea cunoștințelor pe tema: „Patrulaterul“; dezvoltarea abilităților de bază.
• Educațional - să dezvolte o atenție, diligență, perseverență, gândirea logică, vorbire matematică elevilor.
• Educațional - prin tutorial pentru a educa o atitudine atentă unii față de alții, pentru a da posibilitatea de a asculta la prieteni, asistență reciprocă, auto-suficiență.

obiectivele lecției

• Dezvoltarea abilităților de a construi un patrulater cu ajutorul unei bare la scară și un desen al unui triunghi.
• Verificați capacitatea elevilor de a rezolva probleme.

plan de lecție

1. Informații istorice. geometria non-euclidiana.
2. Cadrilaterul de.
3. Tipuri patrulatere.
4. paralelogram
5. Dreptunghi.
6. Rhombus.
7. Square.
8. Trapez.
9. Deltoids.

Geometrii neeuclidiene

Geometria non-euclidiană, a cărui geometrie este similară cu geometria euclidiană care acestea sunt definite cifrele de mișcare, dar diferită de geometria euclidiană prin aceea că unul dintre cele cinci postulatelor sale (a doua sau a cincea) se înlocuiește cu negația. Refuzul unuia dintre postulatele euclidiene (1825) a fost un eveniment important în istoria gândirii, așa cum a fost primul pas spre relativitatea kteorii.

Al doilea postulat al lui Euclid afirmă că orice linie dreaptă poate fi continuată la infinit. Euclid se pare că a crezut că acest postulat conține afirmația că linia are o lungime infinită. Cu toate acestea, geometria „eliptic“ orice linie este finit și, la fel ca cercul este închis.

Al cincilea postulat afirmă că, dacă o linie dreaptă intersectează două linii de date, astfel încât cele două unghiuri interioare, pe de o parte a ei în valoare de mai puțin de două unghiuri drepte, cele două linii drepte, dacă le continua pe termen nelimitat, se întâlnesc pe acea parte, în cazul în care suma acestor unghiuri sunt mai mici decât suma două drepte. Dar, în CB direct „hiperbolic“ geometrie (vezi. Fig.) S-ar putea să fie perpendiculară pe punctul C la dat linia r drepte și se intersectează o altă linie s la un unghi ascuțit la punctul B, dar liniile totuși infinite r și s nu se va întâlni .

Din aceste postulate revizuite a urmat suma unghiurilor unui triunghi este egală cu 180 ° în geometria euclidiană, mai mare de 180 °, într-o geometrie eliptică și mai mică de 180 ° în geometria hiperbolică.

patrulater

Patrulatera - un poligon care conține patru vârfuri și patru laturi.

Cadrilaterul de. figură geometrică - un poligon cu patru colțuri, precum și orice obiect, aparatul acestei forme.

Două fețe neadiacente ale patrulaterului numite opus. Două noduri care nu sunt adiacente, sunt, de asemenea, numite opuse.

Patrulatere convexe (ca ABCD) și
nonconvex (A1 B1 C1 D1).

tipuri de patrulatere

• Paralelogramul - patrulater ale cărei laturi opuse sunt paralele;
  
• Dreptunghi - un patrulater în care toate unghiurile sunt unghiuri drepte;
  
• Rhombus - un patrulater, astfel încât toate părțile sunt egale;
  
• Piața - patrulater în care toate unghiurile sunt unghiuri drepte și toate părțile sunt egale;
  
• Trapez - un patrulater în care cele două laturi opuse sunt paralele;
  
• Deltoid - un patrulater în care două perechi de laturi adiacente sunt egale.

paralelogram

Paralelogramul este numit un patrulater ale cărui laturi opuse sunt paralele.

Paralelogram (din parallelos greacă -. Paralel și gram - line) .. Adică, se află pe linii paralele. Cazuri speciale ale unui paralelogram este un dreptunghi, un pătrat și un diamant.

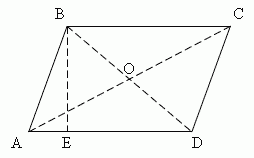
• laturile opuse sunt egale;
• unghiurile opuse sunt egale;
• diagonală bisect punctul de intersecție;
• suma unghiurilor, adiacent de o parte este de 180 °;
• suma pătratelor diagonalelor este egal cu suma pătratelor tuturor părților.

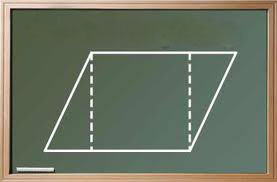
Un patrulater este un paralelogram dacă:

1. Două laturi opuse sunt egale și paralele.
2. laturile opuse sunt egale.
3. Unghiurile opuse sunt egale.
4. punctul de intersecție diagonală împărțită în jumătate.
   

dreptunghi

Dreptunghiul este numit un paralelogram în care toate unghiurile sunt unghiuri drepte.

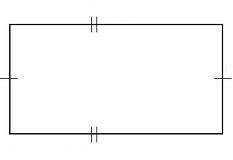
• laturile opuse sunt egale;
• unghiurile opuse sunt egale;
• diagonală bisect punctul de intersecție;
• suma unghiurilor, adiacent de o parte este de 180 °;
• suma pătratelor diagonalelor este egal cu suma pătratelor tuturor părților;
  
• diagonalele sunt egale.
  

1. Unul dintre colțuri drepte.
2. diagonalele sale sunt egale.
   

Un diamant este numit un paralelogram în care toate părțile sunt egale.

• laturile opuse sunt egale;
• unghiurile opuse sunt egale;
• diagonală bisect punctul de intersecție;
• suma unghiurilor, adiacent de o parte este de 180 °;
• suma pătratelor diagonalelor este egal cu suma pătratelor tuturor părților;
• diagonal perpendiculare;
• diagonalele sunt Bisectoarele unghiurilor sale.
  

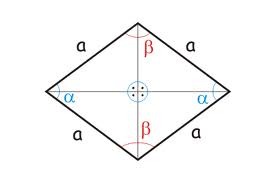
Un paralelogram este un romb, în ​​cazul în care:

1. Cele două laturi adiacente sunt egale.
2. diagonalele sale sunt perpendiculare.
3. Unul dintre diagonalele bisects unghiul acestuia.
   

Piața se numește un dreptunghi. în care toate părțile sunt egale.

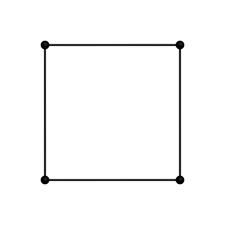
• toate colțurile pătrat drepte;
• diagonala unui pătrat sunt egale, reciproc perpendiculare, punctul de intersecție sunt împărțite în jumătate și se împarte colțurile pătrat în jumătate.

1. Dreptunghi este un pătrat, dacă are vreun indiciu de diamant.

Trapeze numit patrulater ale cărui două părți opuse, sunt paralele, iar celelalte două nu sunt paralele.

laturile paralele ale trapezului sunt numite bazele sale, iar partea neparalele - flancurilor. Segmentul care conectează mijlocul laturilor, se numește linia de mijloc.

Se numește trapez isoscel (sau echilateral), în cazul în care laturile sale sunt egale.

Trapez, un colț, care este o linie dreaptă, numită dreptunghiular.

• linia de centru paralelă la bazele și este egală cu jumătate din suma acestora;
• dacă trapezului isoscel, diagonalele sunt egale și colțurile sale sunt la bază;
• în cazul în care trapez isoscel, cu privire la aceasta este posibil să se descrie un cerc;
• în cazul în care cantitatea de bază este suma laturilor, atunci este posibil să se înscrie într-un cerc.

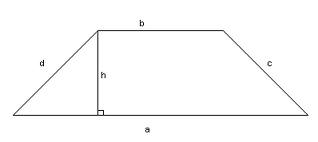
1. Un patrulater este un trapez dacă laturile paralele nu sunt egale

Deltoid - patrulater având două perechi de laturi de lungime egală. Spre deosebire de paralelogram sunt egale nu opuse, și două perechi de laturi adiacente. Deltoid are o formă similară cu un zmeu.

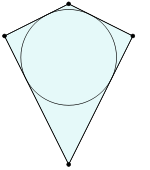
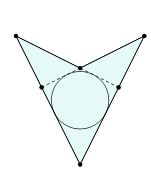
• Unghiurile dintre laturile au lungimi inegale.
• deltoid Diagonal (sau extensiile lor) se intersectează în unghiuri drepte.
• În orice cerc deltoid convexe poate fi înscris, în plus, în cazul în care deltoidul nu este un diamant, există un alt cerc pentru continuarea toate cele patru laturi. Pentru deltoid non-convexe se poate construi o tangentă cerc la cele două părți mari și extinderi ale celor două părți mai mici și o tangentă cerc la cele două părți mai mici și extinderi ale celor două mari partide.
  

• Dacă unghiul dintre laturile inegale linie deltoid, cerc, atunci acesta poate fi înscris (deltoid descris).
• Dacă o pereche de laturi opuse ale deltoidul sunt egale, astfel deltoid este un romb.
• Dacă o pereche de laturi opuse și ambele diagonale sunt egale cu deltoidul, deltoidul este un pătrat. Și un pătrat cu un deltoid înscris diagonalele egale.

fapt interesant

geometria Apariție datează din cele mai vechi timpuri și a fost cauzat nevoile practice ale activității umane (măsurarea volumelor necesitate de măsurare a terenurilor de diferite organisme și t. D.).

informații și concepte geometrice simple au fost cunoscute în Egiptul antic. În această perioadă, declarațiile geometrice formulate sub formă de reguli, să nu probe.

Cu secolul VII î.Hr.. e. I n de vârstă. e. Geometria ca știință a dezvoltat rapid în Grecia antică. În această perioadă, nu numai acumularea de diverse informații geometrice, dar, de asemenea, de a dezvolta metode de dovezi geometrice ale declarațiilor, precum și o primă încercare de a formula poziția de primar de bază (axiome) geometria care raționament pur logic prezentat o varietate de diferite declarații geometrice. Nivelul de dezvoltare al geometriei în Grecia antică se reflectă în compoziția „elemente“ lui Euclid.

În această carte prima dată a fost făcută o încercare de a da o construcție sistematică a geometriei plane, pe baza unor concepte geometrice de bază nedefinite și axiome (postulate).

Un loc aparte în istoria matematicii a luat al cincilea postulat lui Euclid (axioma despre linii paralele). Pentru o lungă perioadă de timp matematicieni au încercat fără succes să aducă al cincilea postulat de celelalte postulate ale lui Euclid, și numai în mijlocul secolului al XIX-lea, datorită cercetării N. I. Lobachevskogo, Riemann și J. Bolyai a devenit clar că al cincilea postulat nu poate fi dedusă din celelalte, iar sistemul de axiome, Euclid a propus, nu numai posibil.

„elemente“ ale lui Euclid au avut o influență enormă asupra dezvoltării matematicii. Această carte este pentru mai mult de două mii de ani, a fost nu numai un manual de geometrie, dar, de asemenea, a servit ca punct de plecare pentru o mulțime de cercetări matematice, ceea ce a dus la orice nouă ramură independentă a matematicii.

Construcția sistematică a geometriei este de obicei făcută în conformitate cu următorul plan:

I. Liste concepte geometrice de bază, care sunt introduse fără definiții.

II. Având în vedere modul de redactare a axiomele geometriei.

III. Pe baza axiomelor și a conceptelor geometrice de bază sunt prezentate concepte și alte teorema geometrică.

1. Originea numelui geometriei non-euclidiene?
2. Cifrele de cacao sunt numite patrulater?
3. Proprietăți paralelogramma?
4. Tipuri de quad-uri?

bibliografie

Am lucrat la lecție

Ridicați problema educației moderne, pentru a exprima o idee sau pentru a rezolva problema în picioare, puteți la Forumul Educațional. în cazul în care educația internațională va bord cu gânduri și acțiuni proaspete. Prin crearea unui blog, va spori nu numai statutul său ca un instructor calificat, dar, de asemenea, aduce o contribuție semnificativă la dezvoltarea școlii viitoare. Liderii Alianței Educație își deschide porțile pentru profesioniștii din cel mai înalt rang, și invită să coopereze pentru crearea celor mai bune școli din lume.