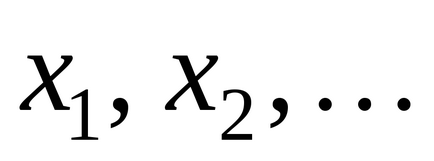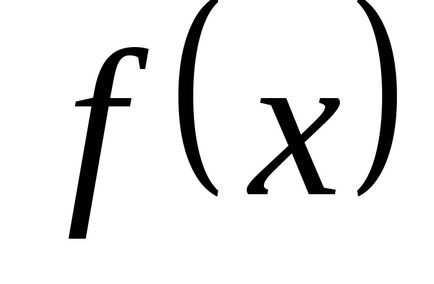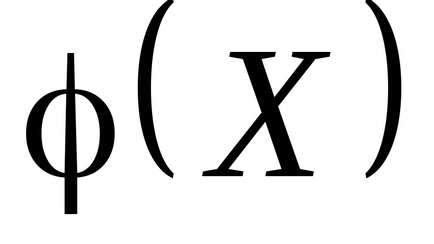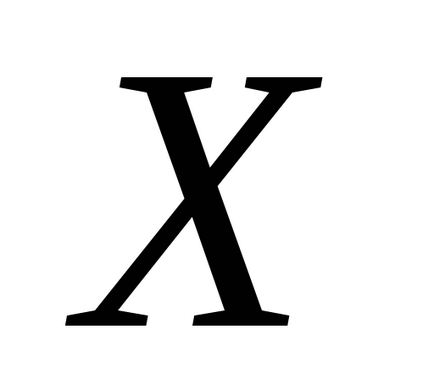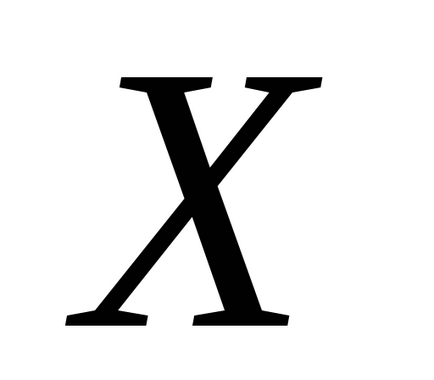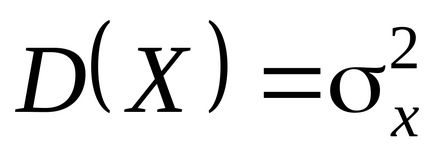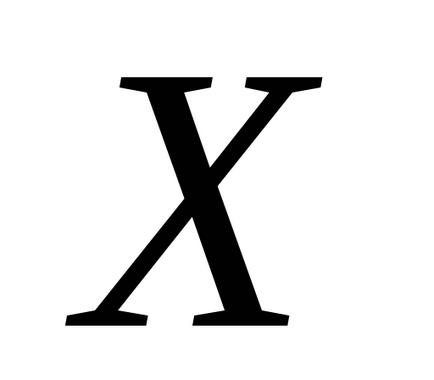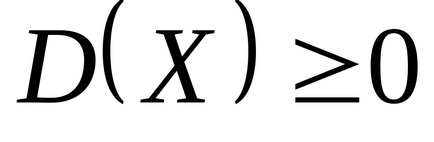Prin caracteristicile numerice ale variabilelor aleatoare includ: așteptări, varianța, momentele de diferite ordine, etc.
lăsa
- variabile aleatoare discrete luând valori
cu probabilități
respectiv.
Așteptări (st) sau dm valoare medie
este numărul
pe ipoteza că seria converge absolut.
Dacă numărul
divergent, atunci spunem că SV
Are finit st
dacă
- variabile aleatoare continue cu o densitate de probabilitate
, apoi st definit de integrala
cu condiția ca converge absolut.
lăsa
- variabile aleatoare discrete cu legea de distribuție (2.1) (Subiect: variabile aleatoare scalare), și
- funcția de rulotă Apoi, legea distribuției variabilelor aleatoare
Ea are forma tabelului. 7.1 (Subiect: variabile aleatoare Scalar). Conform ecuației (1.1) st variabilă aleatoare
definită prin formula
.
În cazul în care, cu toate acestea,
- variabile aleatoare continue cu o densitate de probabilitate
, că generalizând argumentele anterioare, obținem o formulă pentru OM variabilă aleatoare
sub forma
Exemplul 1.1. Numerarul tombolă 200 de bilete emise. A jucat un câștig în valoare de 50 de ruble. doi - la 25 de ruble. zece - 1 freca. Găsiți valoarea medie câștig în cazul în care a cumpărat un bilet.
Conform exemplului D 2.1 (Subiect: valori aleatoare Scalare) d.s. lege de distribuție
- câștig - este (2.2) (Subiect: Variabile aleatoare Scalar).
Conform formulei (1.1), valoarea medie a câștiga
Deci, câștigul mediu la loterie este egal cu 55 de copeici. ▲
Exemplul 1.2. funcția de densitate de probabilitate a variabilelor aleatoare
arată
Conform formula D (1.3)
. ▲
Să ne explicăm proprietățile de bază ale așteptărilor.
1 0. MO numărul de apariții ale unor evenimente
într-un test de probabilitate egală
acest eveniment.
2 0. MO nonrandom valoare constantă
este
.
3 0. nonrandom multiplicator constant
Acesta poate fi luat ca un semn al așteptărilor.
4 0. Pentru orice variabile aleatoare (dependentă sau independentă) st suma SV
și
egală cu suma OM aceste valori:
5 0. Pentru variabilele aleatoare independente st lucrări SV
și
egală cu produsul dintre st de SV și anume
Exemplul 1.3. Găsiți MO suma numărului de puncte care pot cădea atunci când aruncă două zaruri.
Fie D
și
- numărul de puncte a scăzut pe prima și a doua oase, respectiv. Variabile aleatoare discrete
și
ia valorile 1, 2, 3, 4, 5 și 6, cu aceeași probabilitate
. Apoi, prin (1.4) și (1.1) necesar MO
. ▲
MO Se caracterizează dm valoarea medie abaterea SV
din așteptarea matematică (medie) .. De multe ori numit valoarea SV
nazyvaetsyatsentrirovannoy SV
Dispersia sau împrăștiere
variabilă aleatoare
Este o așteptare matematică a abaterii pătrat a variabilei aleatoare
de la așteptările sale matematice:
Rădăcina pătrată a varianței se numește medie pătratică (pătratic) Abaterea d.s.
și este notat
, astfel încât
.
Pentru variabilele aleatoare discrete
, luând valori
probabilitate
,
, dispersia este determinată prin ecuația
Pentru variabile aleatoare continue
dispersia este determinată prin ecuația
în cazul în care există această integrantă. aici
- dm densitate de probabilitate
.
Din proprietățile MM și determinarea dispersiei au
.
Deci, pentru variabile aleatoare discrete
Pentru variabile aleatoare continue
(2.4) are forma
Formulele (2.4) și (2.5) sunt mai convenabile pentru a calcula dispersia.
Notă. Din definiția dispersiei (2.1) d.s.
rezultă că
. Dacă varianța este mică, atunci fiecare termen al sumei (2.2), este de asemenea mic. Prin urmare, valoarea
, în care
mare, ar trebui să aibă o probabilitate redusă. Cu alte cuvinte, cu mici abateri mari de dispersie D.S.
de la MO ei
puțin probabilă. egalitate
înseamnă că
pentru acele valori
, probabilitate
este egală cu zero. Cu alte cuvinte,
înseamnă că
cu unitate de probabilitate.
Exemplul 2.1. Găsiți variația rulotă
, având în vedere legea de distribuție a probabilității