Găsiți raza cercului. Raza - un segment care conectează centrul cercului la orice punct de pe circumferința exterioară a cercului. Raza poate fi măsurată în orice direcție, ar fi la fel. Raza este de asemenea egală cu jumătate din diametrul cercului. Diametrul - este segmentul care trece prin centrul cercului și leagă două puncte de circumferința exterioară a cercului. [1]
- Ca o regulă, valoarea razei dată în problema. Destul de dificil de a găsi centrul exact al cercului, cu excepția cazului în care este marcată în cerc, care este desenată pe hârtie.
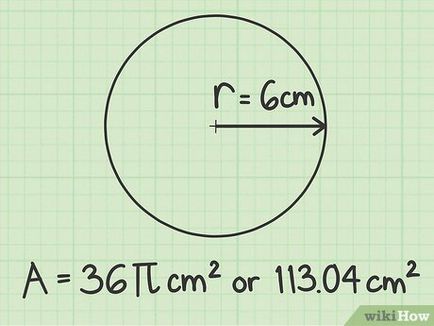
- De exemplu, raza cercului este de 6 cm.
Ridicați raza la pătrat. Formula de calcul a ariei unui cerc: S = π r 2>. unde r - raza care este ridicat în al doilea grad (pătrat). [2]
- Nu este nevoie să cvadratura întreaga formulă.
- In exemplul nostru: r = 6. Prin urmare, r 2 = 36 = 36>.
Rezultatul obținut se înmulțește cu numărul Pi. Acest număr este notat cu litera grecească tt și este o constantă matematică ce caracterizează relația dintre raza cercului și pătrat. Pi este aproximativ egal cu 3,14. Valoarea exactă a Pi include un număr infinit de cifre. Uneori răspuns (suprafața unui cerc) înregistrat cu o π constantă. [3]
- În exemplul nostru (r = 6 cm) pătrat se calculează după cum urmează:
- S = π r 2>
- S = π 2 iunie>
- S = 36 și S = π 36 (3. 14) = 113. 04
Notați răspunsul. Amintiți-vă că zona este măsurată în unități pătrate. Dacă raza este dată în centimetri, suprafața măsurată în centimetri pătrați. Dacă raza este dată în milimetri, suprafața măsurată în milimetri pătrați. Verificați cu instructorul, dacă doriți să prezinte un răspuns la tt constantă, sau sub formă numerică, folosind o valoare aproximativă de pi. În cazul în care cererea nu este clar, să facă o notă de două răspunsuri. [4]
- În exemplul nostru (r = 6 cm) S = π 36 cm 2 sau S = 113,04 cm2.
Înregistrare convertit formulă. Dacă lungimea circumferința cercului este cunoscută, putem folosi formula de calcul a transformat aria sa. Această formulă include lungimea pe circumferință și raza nu sunt, și este scris ca:
Se măsoară și se înregistrează circumferința. În unele situații, este imposibil să se măsoare cu precizie diametrul sau raza. În cazul în care diametrul nu este desenată sau centru nu este marcat, este foarte dificil de a găsi centrul exact al cercului. Circumferința unor obiecte (de exemplu, pansa) este destul de ușor de măsurat cu o măsură de bandă, este posibil să se găsească o valoare mai precisă a circumferinței decât diametrul. [5]
- De exemplu, lungimea circumferința unui cerc (sau obiect rotund) este de 42 cm.
Utilizați raportul dintre lungimea și raza cercului de a rescrie. Circumferința este egal cu numărul Pi pe diametru. Acesta poate fi scris ca: C = π d. Să ne amintim că un diametru egal cu dublul razei, adică d = 2 r. Se combină aceste ecuații, pentru a arde următoarea formulă: C = π 2 r. Acum izola r variabilă. [6]
- C = π r 2
- C 2 π = r> = r> (divide ambele părți cu 2 π)
Se înregistrează formula de calcul suprafața unui cerc. Înregistrarea convertită formulă bazată pe raportul dintre lungimea și raza cercului. Substitut ultima egalitate în formula standard pentru calcularea ariei unui cerc: [7]
- S = π r 2> (formula standard)
- S = π (C 2 π) 2>)> (r expresie în loc încadrată)
- S = π (C 04 februarie π 2) >>>)> (construită într-o fracție pătrat)
- S = C 2 aprilie π >>> (π redus în numărătorul și numitorul)
Utilizați formula convertit pentru a rezolva problema. Acum, în formula în loc de raza circumferinței este prezent, prin urmare, este posibil să se calculeze aria unui cerc de circumferință cunoscut. Se pune o valoare de lungime și circumferință a efectua calcule după cum urmează: [8]
- In exemplul nostru, C = 42 cm.
- S = C 2 aprilie π >>>
- S = 42 02 aprilie π >>> (valoare încadrată)
- 1764 S = 4 π >> (calculat 42 2)
- S = 441 π >> (împărțit la 4)
Notați răspunsul. Dacă lungimea circumferențiară este dată ca număr, nu un produs al numărului și tt. răspunsul poate fi scris π în numitor. Sau în loc să înlocuiască Pi valoarea aproximativă (3.14). [9]
- În exemplul nostru (C = 42 cm) S = π >> 441 cm2.
- Sau ca: S = 441 π = 441 3. 14 = 140. 4> => = 140.4> cm2.