Cum să demonstreze că patrulaterul - un paralelogram, triunghiuri

Cum să demonstreze că patrulaterul - un paralelogram? Puteți utiliza definiția oricăreia dintre semnele unui paralelogram.

1) Un patrulater este un paralelogram, prin definiție, dacă se opune laturi sunt paralele, și anume se află pe linii paralele.

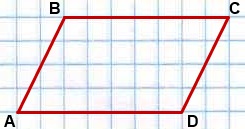
ABCD - un paralelogram dacă

Pentru a dovedi liniile paralele folosind una din caracteristicile liniilor paralele. cel mai adesea - prin unghiuri interne în cruce mincinoase. Pentru a dovedi că unghiurile interne în cruce mincinoase se poate dovedi că o pereche de triunghiuri.

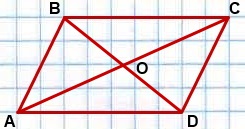
De exemplu, aceasta poate fi o pereche de triunghiuri

Pentru a utiliza această caracteristică a paralelogramului, trebuie să dovedească mai întâi că AO = OC, BO = OD.

Pentru a utiliza această caracteristică a paralelogramului, noi trebuie să dovedească mai întâi că AD = BC și AD ∥ BC (sau AB = CD si AB ∥ CD).

Pentru a face acest lucru, puteți dovedi că una din aceleași perechi de triunghiuri.

Pentru a profita de această caracteristică a paralelogramului trebuie să dovedească mai întâi că AD = BC si AB = CD.

Pentru a demonstra această egalitate de triunghiuri ABC si CDA sau BCD și DAB.

Aceasta - cele patru modalități principale pentru a dovedi că un anumit patrulater - un paralelogram. Există și alte modalități de a dovedi. De exemplu, un dreptunghi - un paralelogram în cazul în care suma pătratelor diagonalelor este egal cu suma pătratelor părților. Dar, pentru a profita de caracteristici suplimentare, trebuie să le dovedească mai întâi.

Dovada folosind vectori sau coordonează, de asemenea, se bazează pe definirea și caracteristicile unui paralelogram, dar realizat în mod diferit. Această întrebare va fi efectuată în vectori de subiecte și coordonate carteziene.