Cum de a găsi unghiul dintre cei doi vectori

Vector - un segment cu o anumită direcție. Unghiul dintre vectori este o valoare fizică, cum ar fi atunci când lungimea vectorului proiecției pe axa.

Unghiul dintre cei doi vectori nenuli este determinată prin calcularea unui produs scalar. Prin definiția produsului scalar este produsul dintre lungimile vectorilor la cosinusul unghiului dintre ele. Pe de altă parte, produsul scalar a doi vectori cu coordonatele (x1, y1) și coordonatele b (x2; y2) se calculează cu formula: ab = x1x2 + y1y2. Dintre aceste două metode de a găsi produsul scalar este ușor de a găsi unghiul dintre vectorii.

Găsiți lungimea vectorilor sau a modulelor. Pentru vectorii noștri și b: | o | = (X1² + y1²) ^ 1/2 | b | = (X2² + y2²) ^ 1/2.

Găsiți produsul scalar al vectorilor, multiplicând poziția lor în perechi: ab = x1x2 + y1y2. Din definiția produsului scalar ab = | A | * | b | * cos # 945;, unde # 945; - unghiul dintre vectori. Apoi am descoperit că x1x2 + y1y2 = | A | * | b | * cos # 945;. apoi cos # 945; = (X1x2 + y1y2) / (| a | * | b |) = (x1x2 + y1y2) / ((x1² + y1²) (x2² + y2²)) ^ 1/2.

găsi unghiul # 945; folosind tabele Bradis.

În cazul spațiului tridimensional se adaugă la a treia coordonate. Pentru vectorii a (x1, y1, z1) și b (x2; y2; z2) formula pentru cosinusul unghiului prezentat în Fig.

produsul scalar - este un scalar lungimi caracteristice ale vectorilor și unghiul dintre ele.

Avionul - unul dintre conceptele de bază din geometrie. Avionul este o suprafață pentru care afirmația este adevărată - orice linie care leagă două puncte de sale deținute în întregime de această suprafață. Avionul poate fi desemnate prin literele grecești a, β, γ, etc. Două avioane se intersectează întotdeauna într-o linie dreaptă, care face parte din ambele planuri.

Să considerăm grupa a semiplanului și p formate prin intersecția a două plane. Unghiul format printr-o linie dreaptă și două jumătăți de avioane alfa și β se numește unghiul diedru. In aceasta formând un diedru numite fațete semiplanului, o linie de intersecție a planului unghiului diedru se numește o margine.

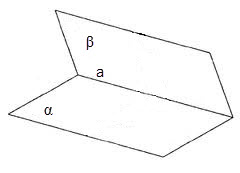
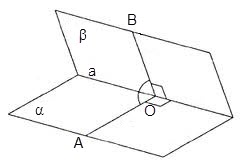
Diedrului unghi ca unghiul plan, măsurat în grade. Pentru a măsura unghiul diedru este necesar pe fețele sale pentru a alege un punct arbitrar O. In ambele planuri care trec prin O sunt realizate două grinzi perpendiculare pe marginea unui. Unghiul format AOB numit diedru unghi liniar, cu o margine a unui.

Astfel, măsurarea unghiului dintre două planuri care se intersectează α și unghiul p care trebuie măsurat ∠AOB liniar.

Geometria Vector se numește un segment de linie direcționat sau o pereche ordonată de puncte dintr-un spațiu euclidian. Lungimea vectorului - un scalar egal cu rădăcina pătrată a sumei aritmetice a pătratelor coordonatele (componente) ale vectorului.

• Cunoștințe de bază de geometrie și algebră.

Cosinusul unghiului dintre vectori este găsit de produsul lor scalar. Suma produselor componentelor corespunzătoare ale vectorului egal cu produsul dintre lungimile lor de cosinusul unghiului dintre ele. Lăsați cei doi vectori sunt: ​​(x1, y1) și b (x2, y2). Apoi, produsul scalar poate fi scrisă sub forma egalității: x1 * x2 + y1 * y2 = | A | * | b | * cos (U), unde U - unghiul dintre vectori.

De exemplu, coordonatele vectorului a (0, 3) și b vectorul (3, 4).

Exprimandu obținut din cos ecuația (U) este obținut, care cos (U) = (x1 * x2 + y1 * y2) / (| a | * | b |). În exemplul formulei după înlocuirea coordonatelor cunoscute iau forma: cos (U) = (0 * 3 + 3 * 4) / (| a | * | b |) sau cos (U) = 12 / (| a | * | b | ).

Lungimea vectorilor este de formulele: | A | = (X1 ^ 2 + y1 ^ 2) ^ 1/2, | b | = (X2 ^ 2 + y2 ^ 2) ^ 1/2. Substituind ca și coordonatele vectorilor de (0, 3), b (3, 4) se obține, respectiv, | a | = 3 | b | = 5.

Substituind aceste valori în formulă cos (U) = (x1 * x2 + y1 * y2) / (| a | * | b |), pentru a primi răspunsul. Utilizarea vectorilor de lungime detectate vor primi ca cosinusul unghiului între (0, 3), b (3, 4), este egal cu: cos (U) = 12/15.

Dacă toate numărate corect, cosinusul unghiului ar trebui să fie mai mică decât unu. Ca vectori de lungime nu poate fi negativ.

Dacă lungimea unuia dintre vectorii este egal cu zero, atunci este un vector de zero, iar apoi unghiul dintre vectorul și celălalt este de 90 de grade.

Vector - segmentul de linie îndreptate având o anumită lungime. În spațiu, este definit de trei proiecții pe axele respective. Este posibil de a găsi unghiul dintre vectorul și planul. în cazul în care este reprezentată prin coordonatele normale sale, și anume, ecuația generală.

Avionul - aceasta este figura principală a geometriei spațiale, care este implicată în construirea formelor bidimensionale și tridimensionale, cum ar fi triunghiuri nik, pătrat, paralelipiped, prisme, cerc, elipsa, etc. În fiecare caz, este limitată la anumite set de linii care se intersectează pentru a forma o formă închisă.

În general, un plan care nu este limitat de nimic, se extinde pe fiecare parte a imaginii sale în mod direct. Această formă plată fără sfârșit, care, cu toate acestea, poate fi dată de ecuația, adică numere finite, care sunt coordonatele vectorului normal.

Pe baza celor de mai sus, este posibil să se găsească unghiul dintre vectorul și orice plan. utilizând formula de cosinusul unghiului dintre doi vectori. segmentele dirijate pot fi poziționate în spațiu așa cum se dorește, totuși, fiecare vector are o astfel de proprietate care poate fi mutat fără pierderea caracteristicilor esențiale ale acestora, direcția și lungimea. Și este necesar să se utilizeze pentru a calcula unghiul dintre vectorii distanțate prin plasarea lor într-un punct de plecare vizual.

Astfel, să presupunem că, având un vector V = (a, b, c) și planul A • x + B • y + z = 0, C • unde A, B și C - coordonatele N. normale Apoi cosinusul unghiului α dintre vectorii V și N este egal cu: cos α = (a • a + b • b + a • C) / (√ (a² + b² + s²) • √ (a² + V² + C²)).

Pentru a calcula unghiul în grade sau radiani, trebuie să se calculeze expresia rezultată a inversului cosinusul, adică arccosinus: α = arssos ((A • A + b • B + a • C) / (√ (a² + b² + s²) • √ (A² + V² + C²))).

Exemplu: obține unghiul dintre vectorul (5, 3, 8) și planul. dat ecuația generală 2 • x - 5 • y + z = 3 • 0.Reshenie: descărcarea vectorul normal al planului coordonatele N = (2, -5, 3). Substitut toate valorile cunoscute în formula de mai sus: cos α = (10 + 15 + 24) / √3724 ≈ 0,8 → α = 36,87 °.

Valori de măsurare a unghiului plan în grade a fost inventat în Babilonul antic cu mult înainte de era creștină. Locuitorii acestui stat preferă sistem numărul șaizecelea, astfel încât unghiurile de diviziune a 180 sau 360 de unități acum pare un pic ciudat. Cu toate acestea, stau în sistem modern de unități SI, care sunt multipli de pi, nu mai puțin ciudat. Aceste două opțiuni nu sunt limitate la unghiuri de denumiri utilizate în prezent, astfel încât sarcina de a traduce valorile lor în măsură gradusnuju apare destul de des.

În cazul în care gradusnuju măsură este necesară pentru a traduce unghiul în radiani, presupunem că un grad corespunde numărului de radiani egal cu 1/180 fracție Pi. Această constantă matematică are un număr infinit de zecimale, deci un factor de conversie de la radiani în grade este, de asemenea, o fracție zecimală fără sfârșit. Acest lucru înseamnă că valoarea absolut exactă în format zecimal nu ieși, astfel încât factorul de conversie care urmează să fie rotunjite. De exemplu, cu o precizie de o miliardime a raportului calculat este egal cu unitatea 0.017453293. După rotunjirea numărul necesar de cifre, se împarte la acest factor numărul inițial de radiani, și veți obține un unghi de măsură de grade.

În rezolvarea problemelor matematice ale secțiunilor referitoare la geometrie, formula frecventă, în care unghiurile sunt exprimate nu radiani, și acțiuni ale Pi. Dacă obțineți o soluție care conține această constantă, pentru a converti în grade înlocui numărul π 180. De exemplu, dacă unghiul central de definit prin expresia π / 4, aceasta înseamnă că o măsură de gradul său este de 180 ° / 4 = 45 °.

Colțuri pot fi exprimate și unități care sunt numite „revoluție“. Această unitate corespunde la 360 °, astfel încât să apară problemele cu conversie. De exemplu, dacă setarea unghiului de stări la o jumătate de rotație, aceasta corespunde la 1,5 * 360 = 540 ° în măsurători cu arc.

Uneori, unghiul drept se referă la probleme geometrice. Acesta este format din două grinzi în direcții opuse, care este, situată pe o linie dreaptă. Utilizați numărul 180 pentru exprimarea valorii unghiului drept în grade.

În geodezie, cartografie, grade de astronomie sunt împărțite în unități mai mici, care au propriile lor nume - minute și secunde. Această divizare are rădăcinile în același loc și grade, astfel încât fiecare grad include 60 de minute, sau 3600 secunde. Utilizați aceste numere atunci când secunde și minute trebuie să fie înlocuită cu zecimi de grad. De exemplu, unghiul de 11 ° 14'22 „corespunde cu fracția zecimală este aproximativ egală cu 11 + 14/60 + 22/3600 ≈ 11,2394 °.

vector în spațiul multidimensional este definit de coordonatele punctului său de pornire și punctele care definesc magnitudinea și direcția sa. Diferența dintre cele două direcții de vectori determinați valoarea unghiului. De multe ori, în tot felul de probleme din fizică și matematică sunt invitați să se găsească nu unghiul, iar valoarea derivată din acesta funcții trigonometrice - sine.

Utilizare pentru determinarea sinusaugla între doi vectori cunoscuți formula de vectori de multiplicare scalare. Astfel de formule există ca cel puțin două. Într-una dintre ele ca o variabilă implicată cosinusul unghiului dorit. știind că va fi capabil să calculeze sinusul.

Asigurați-egalitate și să-l izoleze de cosinusul. Conform unei formule de produs scalar al vectorilor este egală cu lungimea lor, înmulțirea reciproc și cu cosinusul unghiului. iar pe de altă parte - suma produselor din coordonatele de-a lungul fiecărei axe. Echivalând ambele formule se poate trage concluzia că cosinusul unghiului ar trebui să fie egală cu o sumă de produse de coordonate relative la produsul dintre lungimile vectorilor.

Se înregistrează ecuația rezultată. Pentru aceasta avem nevoie pentru a identifica coordonatele ambelor vectori. Să spunem că sunt într-un sistem de coordonate cartezian tridimensional și punctele lor de plecare mutat în partea de sus a grilei. Direcția și magnitudinea primului vector va fi dat punct (X₁, Y₁, Z₁), un al doilea - (X₂, Y₂, Z₂), iar litera eticheta unghiului γ. Apoi, lungimea fiecăruia dintre vectorii pot fi calculate, de exemplu, prin teorema lui Pitagora pentru triunghiul format de proiecțiile lor pe fiecare dintre axele de coordonate: √ (X₁² + Y₁² + Z₁²) și √ (X₂² + Y₂² + Z₂²). Substitut aceste expresii în formula formulată în etapa anterioară, și vei obține ecuația: cos (γ) = (X₁ * X₂ + Y₁ * Y₂ + Z₁ * Z₂) / (√ (X₁² + Y₁² + Z₁²) * √ (X₂² + Y₂² + Z₂²)).

Utilizați faptul că suma valorilor pătratele sinus și cosinus unghiului de aceeași magnitudine este întotdeauna da una. Deci, a ridicat obținut în etapa anterioară, expresia pentru cosinusul la pătrat și se scade din unitate, iar apoi găsiți rădăcina pătrată, vă decide problema. Se înregistrează formula dorită într-o formă generală: sin (γ) = √ (1-cos (γ) ²) = √ (1 - ((X₁ * X₂ + Y₁ * Y₂ + Z₁ * Z₂) / (√ (X₁² + Y₁² + Z₁² ) * √ (X₂² + Y₂² + Z₂²)) ²) = √ (1 - ((X₁ * X₂ + Y₁ * Y₂ + Z₁ * Z₂) ² / ((X₁² + Y₁² + Z₁²) * (X₂² + Y₂² + Z₂²) )).

Operații cu vectori cauzează adesea dificultăți pentru elevi. În ciuda disponibilității unui număr limitat de formule cu care să funcționeze, unele sarcini cauzează o complexitate și soluție. În special, nu toți elevii de liceu sunt în măsură să calculeze unghiul dintre vectorii.

Rețineți că calculul unghiului dintre oricare doi vectori este redusă la găsirea unei între vectorii. având un punct comun. Acest lucru face ca de multe ori neînțelegere, dar a explicat pur și simplu. Pentru a doi vectori coplanari începe la un moment dat, trebuie să efectuați o operațiune de transport de paralel. Dar această procedură nu afectează valoarea dorită.

Notă definiția generală a unghiului dintre doi vectori. aceasta vă va ajuta să se stabilească o idee despre ceea ce este necesar în sarcina. Deoarece unghiul - nu este absolut, ci o anumită realitate care indică cel mai scurt prin care să se rotească un vector (în ceea ce privește punctul său de plecare) la codirectional cu al doilea. Este important să se aibă în vedere faptul că valoarea dorită a unghiului trebuie să fie în intervalul de la zero la 3.14 radiani.

Nu uitați că, dacă se face cu coliniare sau vectori paralele. Valoarea unghiului este de zero grade în cazul co-direcțional și 180 - pentru vectorii multidirecționale. Rezultă din definiția, pentru că trebuie să se rotească al doilea vector pentru a schimba direcția sa.

Utilizați formula simpla care permite calcularea rapidă a valorii cosinusul unghiului dintre vectori. Pentru a face acest lucru trebuie să știți coordonatele. Cosinusul unghiului este o fracție în care numărătorul este produsul scalar al vectorilor, iar numitorul - produsul modulelor acestora. Pentru a găsi prima valoare pentru vectorii cu coordonatele a1, a2, a3 și c1, c2, c3, găsi suma produselor A1C1, a2s2, a3s3. Modulus fiecărui vector este rădăcina a doua putere a sumei pătratelor coordonatelor.

Consultați ajutor calculatoare electronice, care specifică parametrii vectorilor calculați unghiul dorit.