Cum de a găsi aria unui triunghi

Uneori, cunoașterea curriculum-ului sunt necesare în viața adultă (de regulă este apare o astfel de necesitate în timpul reparării).

Suprafața unui triunghi pot fi găsite în diferite moduri, în funcție de tipul triunghiului, zona ce căutăm. Orice triunghiuri convenționale (figura planul format prin trei linii intersectate), dreptunghi (unul dintre colțuri este de 90 de grade), isoscel (două dintre marginile sale sunt egale) și echilateral (toate marginile sale sunt egale).

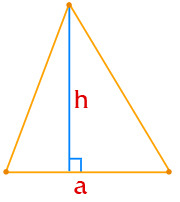
În triunghiul convențional suprafața sa este calculată ca jumătate din produsul din lungimea bazei triunghiului de cantitatea de înălțime este coborâtă la sol cu ​​vârful opus:

în cazul în care zona S-triunghi,

b lungimea unei laturi a triunghiului,

h înălțime, a scăzut la partea.

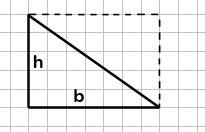
Formula este ușor de ținut minte exemplul zonei unui triunghi dreptunghic (un caz particular de a găsi aria unui triunghi). Zona unui triunghi dreptunghic - este jumătate din suprafața unui dreptunghi imaginar:

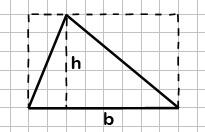
Există o altă modalitate de a calcula aria triunghiului (formula lui Heron) utilizat, dacă se cunoaște lungimea de trei laturi ale triunghiului.

Suprafață egală cu rădăcina pătrată a semiperimetrul produsului și sacristii între laturile semiperimetrul și ale triunghiului:

unde S - zona de triunghi,

p - semiperimetrul: p = (a + b + c) / 2,

a, b, c - laturi (margini) ale triunghiului.

Uneori, în viața oamenilor trebuie să-și amintească de cunoștințe școală uitat lung. De exemplu, în cazul în care următoarea reparație într-o casă sau un apartament este necesar pentru a determina cantitatea de material pe o suprafață de formă triunghiulară. Suprafața unui triunghi este jumătate din produsul ca o lungime de bază triunghi la valoarea înălțimii, coborâtă la o anumită bază din vârful opus. Este scris după cum urmează: S = 1/2 * b * h, în cazul în care zona S-triunghi, b-lungimea unei laturi a triunghiului, h-înălțime, a scăzut la acea parte.

Dintre toate formulele care pot fi folosite pentru a găsi zona oricărui triunghi, dar acestea nu sunt de ajuns, aș dori să atrag atenția deosebită doar două:

S (ABC) = 1 / 2BH unde b - lungimea laterală a înălțimii triunghiului h, a scăzut la acea parte - această formulă este folosit de oameni practicat în 95% din cazuri.

Există cazuri în care este dificil să se determine înălțimea și laturile triunghiului și unghiul dintre ele este ușor de măsurat, în timp ce

Depinde de ceea ce se cunosc parametrii triunghiului.

Cea mai comună formulă - produs din oricare două dintre laturile sale prin sinusul unghiului dintre ele bisect: S = a · b · păcate / 2 = a · c · sinv / 2 = b · c · sina / 2,

a, b, c - care a formulat opoziția acestora.

Zona triunghiului care le-am găsit, așa cum îmi amintesc în școala elementară la geometrie. Mi-a plăcut geometria, îi plăcea să atragă toate formele pentru a găsi soluția problemelor, pentru a demonstra teorema, dar nu a mers mai departe în acest profil.

Deci, aria unui triunghi este egală cu o jumătate de ori înălțimea laturii triunghiului la care această înălțime este coborâtă perpendicular.