cercuri inscriptionare circumscrise

Existența :. Desenați un cerc centrat la $ O $ și rază de $ OK \ $ Deoarece punctul $ O $ este pe trei Bisectors, este echidistant față de laturile triunghiului ABC $ $. Aceasta este de $ OM = OK = OL $. Prin urmare, cercul construit de asemenea, trece prin punctul $ M \ și \ L $. De la $ OM, OK \ i \ OL $ - normalele la laturile triunghiului, atunci teorema de pe tangenta la cercul construit tangenta la toate cele trei laturi ale triunghiului. În consecință, în virtutea arbitrariului triunghiului, triunghiul în orice cerc poate fi înscris.

Unicitatea: Să presupunem că triunghiul de $ ABC $, puteți introduce un alt cerc cu centrul $ O „$. Centrul său echidistant față de laturile unui triunghi, și, prin urmare, coincide cu punctul $ O $ și are o rază egală cu lungimea $ $ OK. Dar, atunci acest cerc va coincide cu prima.

Corolar 1: Centrul cercului înscris în triunghiul se află la intersecția Bisectors sale.

Iată câteva fapte legate de conceptul cercului inscris:

Nu orice patrulater poate fi înscris cerc.

În orice patrulater tangențială suma laturi opuse sunt egale.

Dacă suma dintre laturile opuse ale unui patrulater convex sunt egale, atunci cercul poate fi înscris în ea.

Cercul circumscris

Dacă toate se află pe circumferința unui nod poligon, atunci cercului numit poligon (Fig. 3).

Unicitatea: Să presupunem că unele triunghi $ ABC $ este posibil pentru a descrie un alt cerc cu centrul $ O „$. echidistantă ei din centrul nodurilor triunghi, și, prin urmare, coincide cu punctul $ O $ și are o rază egală cu lungimea $ OC. $ Dar acest cerc coincide cu prima.

Corolar 1: cerc Centrul descris despre un triunghi coincide cu punctul de intersecție al midperpendiculars sale.

Iată câteva fapte legate de conceptul de cerc circumscris:

Despre patrulaterul nu este întotdeauna posibil să se descrie un cerc.

În orice sumă patrulater ciclică a unghiurilor opuse este egal cu $ ^ 0 $.

În cazul în care suma unghiurilor opuse ale unui patrulater este de $ ^ 0 $, apoi în jurul este posibil să se descrie un cerc.

EXEMPLU problema privind conceptul cercului circumscris și inscripționată

In baza de triunghi isoscel este de 8 cm, partea laterală este egală cu 5 cm. Găsiți raza cercului inscris.

Luați în considerare triunghiul ABC $ $. Prin Corolar 1, știm că centrul cercului înscris se află la intersecția Bisectoarele. Bisectors $ AK $ și $ BM $, care se intersectează în punctul $ O $. Desenati perpendiculara OH $ $ la punctul $ O $ pe partea $ BC $. Desen descrie:

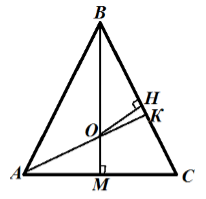
Având în vedere că triunghiul este isoscel, atunci BM $ $ și mediana și înălțimea. Pitagoreic $ ^ 2 ^ 2 ^ 2, \ BM = \ sqrt ^ 2 \ frac ^ 2 >> = \ sqrt = \ sqrt = 3 $. $ OM = OH = r $ - raza dorită a cercului inscris. Deoarece MC $ $ $ și $ segmentelor CH intersectate tangente, apoi teorema pe tangentele intersectându au $ CH = MC = 4 \ $ cm. In consecinta, $ BH = 5-4 = 1 \ $ cm. $ BO = 3-r $. Din triunghiul $ $ OHB, teorema lui Pitagora, obținem: