Aria triunghiului prin zona circumscrisă cercului - cu formula, un calcul exemplu
Un triunghi se numește un înscris, în cazul în care toate nodurile sale se află pe cerc. În acest caz, cercul se numește circumscris în jurul triunghiului.
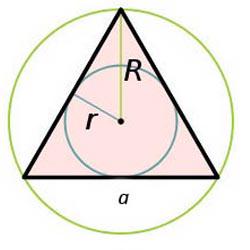
Circumscris se va afla la intersecția midperpendiculars a avut loc la fiecare latură a triunghiului. Dacă cercul este descrisă în jurul unui triunghi dreptunghic, centrul său se va afla în mijlocul ipotenuzei. Pentru fiecare triunghi, cerc descris în jurul căruia acționează zone formulă triunghi cu raza cercului circumscris:
în care a, b, c - partea a triunghiului, și R - raza cercului.
Exemplu de calcul al triunghiului razei cercului circumscris:
Lăsați un triunghi cu laturile a = 5 cm, b = 6 cm, c = 4 cm. In jurul descrie un cerc cu R = 3 cm. Ia zona.
Având toate datele necesare, pur și simplu înlocui valorile în formula:
zonă a unui triunghi este egală cu 10 de metri pătrați. vedea
Destul de des posibil pentru a îndeplini condițiile din această zonă a cercului circumscris care urmează să fie utilizat pentru a găsi triunghi înscris pătrat. zona triunghi Formula printr-un cerc de arie delimitată este după calcularea razei. Acesta poate fi calculat în mai multe moduri. În primul rând, ia în considerare formula pentru aria unui cerc:
Transformarea acestei formule, constatăm că raza:
Folosind această formulă, descoperim că cunoașterea zona cercului circumscris, zona de triunghi pot fi găsite în felul următor:
Știind toate cele trei laturi ale unui anumit triunghi poate fi folosit pentru a găsi zona cu formula lui Heron. Deoarece este posibil să se găsească raza cercului circumscris. Aceasta este, în cazul în care condițiile sunt toate laturile triunghiului și pătrat trebuie să caute prin raza cercului, trebuie mai întâi să-l calcula folosind formula:
Adică, cunoscând lungimile laturilor triunghiului, putem găsi aria unui triunghi cu raza cercului.
Exemplu de calcul al triunghiului prin cercul circumscris zona:
Dan triunghi în jurul valorii de care descrie un cerc cu o suprafață de 8 metri pătrați. Laturile triunghiului cm a = 4 cm, b = 3 cm, c = 5 cm pentru a găsi raza cercului care începe prin zona sa ..:
Să încercăm să găsim raza unei formule diferite, pe care le-am derivat din metoda de a găsi aria unui triunghi pe trei laturi. Semiperimetrul vor găsi:
Înlocuind valori în formula:
Acum vom folosi formula de a găsi aria unui triunghi înscris:
Știind câteva formule simple, am fost capabili de a găsi aria unui triunghi înscris. Acesta va fi egal cu 6 sq. cm.
- Suprafața unui triunghi pe trei laturi
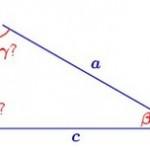
- Suprafața unui triunghi dreptunghic
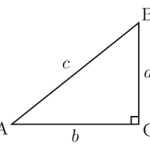
- Aria triunghiului de raza cercului inscris
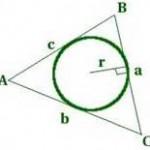
- Raza cercului circumscris hexagonului în jurul valorii de
- Formula lui Heron pentru aria unui triunghi
